ラビットチャレンジ: Stage.4 深層学習 Day3, 4
本ページはラビットチャレンジの、 Stage.4 "深層学習 Day3,4" のレポート提出を兼ねた受講記録です。 提出指示を満たすように、下記の方針でまとめました。
動画講義の要点まとめ (Day3,4)
自分が講義の流れを思い出せるようなメモを残す。通常であれば要点として記載すべき図・数式などがあっても、それが自分にとって既知であれば、言葉の説明ですませることもある
実装演習 (Day.3 のみ)
各Sectionで取り上げられた .ipynb or .py ファイルの内容を実行した結果を記載
ただし、初学者向けにやや冗長な内容がある場合、抜粋することもある
確認テスト (Day.3 のみ)
確認テストの解答に相当する内容は、個別の節をもうけず、要点まとめに含めたり、コードに対するコメントとして記載する
確認テストは重要事項だから、出題されているのであって、まとめ/演習と内容がかぶるはず。
事務局がレポートチェックをする時のために、(確認テスト:1-2) のようなタグを付す。1つ目の数字が section番号、2つ目の数字が 「何番目のテストか?」
1~3 をまとめる上で思うことがあれば、考察やコメントも適宜残しておく。
目次
Day 3
0: CNN の復習
動画 day 3-1 0:00 ~ 18:00
内容は割愛
(確認テスト:0-1) 入力 5x5 フィルタ 3x3 パディング 1 ストライド 2 のとき出力の画像は 3x3
5 + 1*2 - (3-1) = 5 に対して、開始点が 1, 3, 5 と動く
Section.1 : 再帰型 ニューラルネットワークの概念
動画 day 3-1 18:00 - 2:56:30 くらい
RNN (Recurrent Neural Network ) の全体像
時系列データを対象とする
データの並び順に意味があり、観測間隔が一定, かつ 相互に統計的な依存関係が認められるデータ
音声や、テキストデータなど
テキストデータは、単語ひとつひとつを各時刻の観測データとみなす
構造
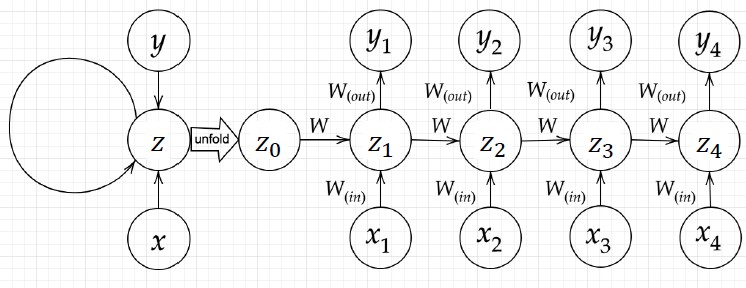
(確認テスト:1-1) RNNのネットワークには、入力層->中間層, 中間層->出力層の他に、前の時刻の中間層->現時刻の中間層の重みがある。
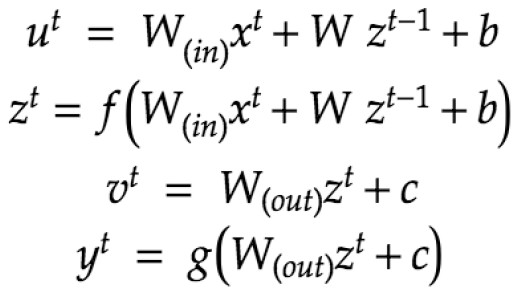
(確認テスト:1-3) の計算式
example
Simple Network は バイナリ加算(2進数同士の足し算) をRNNでやる toy problem
2進数の各桁を各時刻のサンプルと考えて、下から上に順々に処理する
一桁下からの繰り上がり処理が、中間層の再帰に相当
時系列データの頭からお尻までを全部処理したら 1エポック
演習チャレンジ
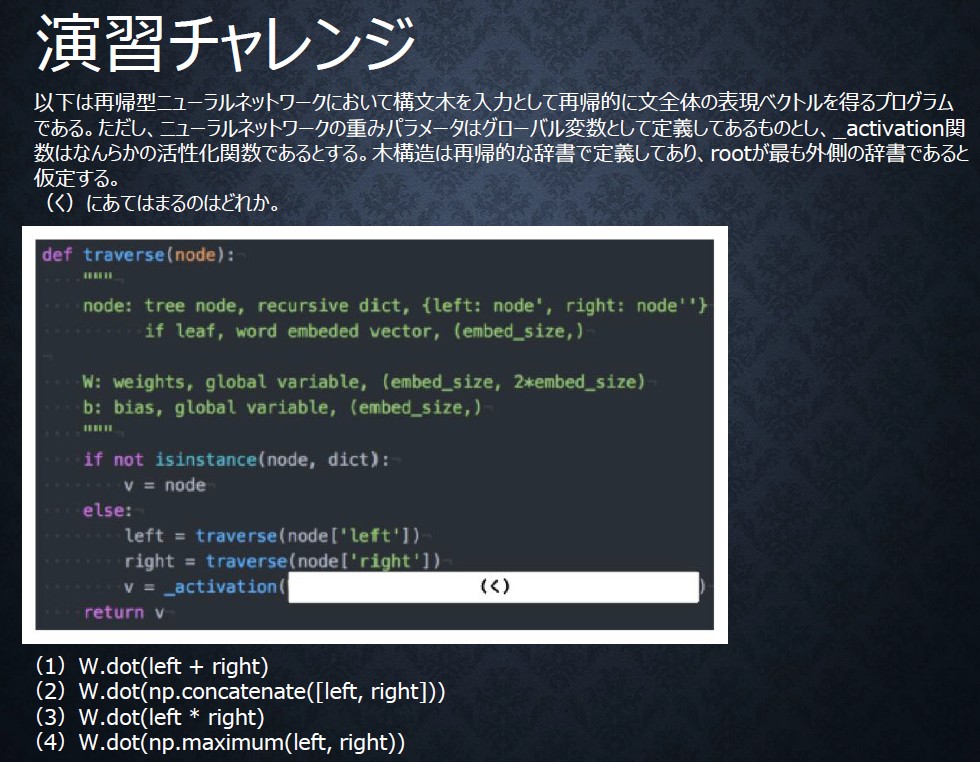
回答は(2)
理由は、"行列W のサイズ (embedsize x 2*embedsize)と矛盾しないのは (2)しかないから" 。
講義ではどういう演算が2つの単語の特徴をうまく統合でるかという論点で解説されているが、そのような解説のアプローチをとるならば 背景知識の説明は構文木でなく embeddingの話などすべきだと思う。
和や積で情報がうまく扱えるか否かは特徴量ベクトルの性質によるので、自然言語処理のこと知らない人がこの話を聞いてもさっぱりで、結局天下りで回答を与えられた印象しか残らない。
BPTT (Back Propagation Through time)
誤差逆伝播の復習
(確認テスト:1-2) のとき
RNNのパラメータ最適化で用いる 誤差逆伝播の一種
ポイントは、時刻t+1 の誤差が 時刻 t の誤差へ逆伝播するところ
以降、自分がわかりやすいよう、導出過程は自分がわかりやすいよう修正する。
MLPはくさるほど計算したが、RNNは昔いっかいやっただけなので、一通り計算しなおしてみる
最初は連鎖律の関係を理解することに注力するため(各ステップの微分でいちいちで次元を気にするのが面倒)に、スカラー前提で計算する
パラメータの更新式をまとめるときにサイズのことを気にした表記にしてみる
BPTTの全体像
評価関数は各時刻でのエラーの和 : と考える
を について展開
... (以下いくらでも を展開していける)
ここからわかること
RNNは無限時間の過去情報を持っている (IIRフィルタといっしょ)
が 複数箇所に出てくる -> それぞれのW の場所まで、誤差逆伝播する必要がある
BPTT の数学的記述(=パラメータ更新式の導出)
パラメータ についてのロスの微分は、 と表せるので、各時刻の微分を考えればよい。
と置く。
のとき (具体的な計算)
と置いた
とする
のとき (具体的な計算 -> 解釈)
二項現れたのは、高校でも学習する関数の積の微分を適用したに過ぎないのだが、この一項目をあえて、 自体が の関数だと思わない場合の微分とみなし、 で書くと、
= (直近の逆伝播経路に起因する項) + (時間をさかのぼった別経路起因の項) と解釈でき、誤差逆伝播の文脈における誤差計算は、パラメータまで伝播する「全ての」経路の総和を取る必要があるということと矛盾しない.
のとき (一般化のための足がかり)
よって、一般の のとき
も同様に考えればよく,
更新式の導出 その 1. ( 実装面, 多次元考慮)
全時刻の情報をバッファせずにパラメータが更新できる.
のため、(実際にはパラメータ自体は時間変化しないのだが) 着目する時間ステップを1つずつ進めながら、 と、誤差項を累積加算するように パラメータ更新が行える
途中で遡る時間を打ち切る
から の が大きくなるほど勾配は小さくなっていくため、長時間遡る経路起因の誤差項は無視できる
そのため、これまで などと書いていた箇所は、所定の時間長 だけ遡ることにして、 と打ち切る
逆に重み によっては勾配爆発の可能性もある。そのための打ち切りということもできる( 勾配消失については打ち切りはよい近似だが、こちらは完全な対症療法)
入力 のサイズを , 隠れ層 のサイズを , 出力 のサイズを とする
のサイズは, のサイズは , のサイズは
スカラー をサイズ のベクトルで微分するので サイズ
は サイズ
よって や と積を取っている部分は更新式における行列のサイズとの関係から、転置をとったベクトル積となる
つまり、講義で講師の先生がいってた発言「の記号は転置でなく、時間を遡って計算する、の意味だ」は間違いだと思われる
以上を考慮して、各パラメータの更新式は下記の通りとなる (下のコード演習問題相当のアルゴリズムが導出できた)
を 1ステップずつ進めながら
さらに 入れ子で から 遡りつつ
本更新式は、以下のコード演習問題の bptt()関数相当の式となっている。
講義中 資料 p.48 の更新式とも見かけ上にているが,,
上記は各時刻 で 各パラメータの に対する勾配を使ってパラメータを更新している.
p.48 では、 に対する勾配を使ってパラメータを更新することになっているが、そのときこの式はただしいんだろうか? 辻褄が合わない気がする
コード演習問題
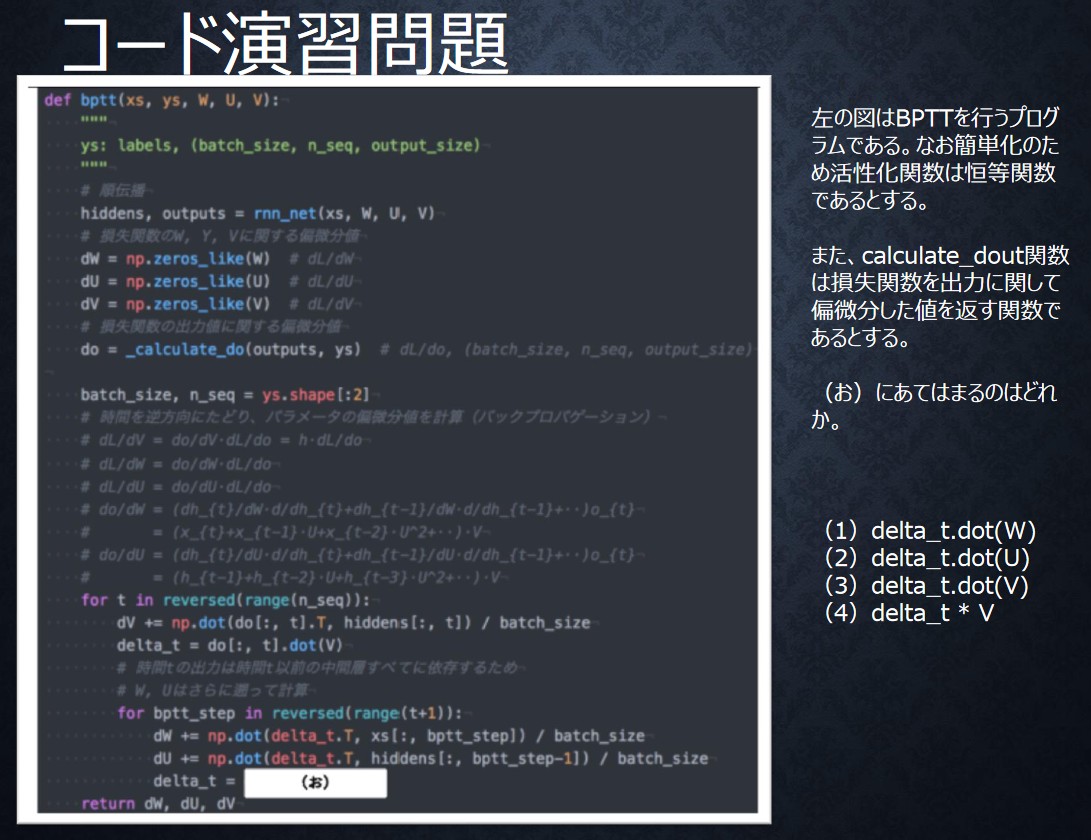
回答:2
問題で埋める部分は、BPTTで時間を遡る を から求めるところ.
現在、1時刻前の中間層出力にかける重みが なので、となる.
更新式の導出 その 2.
その1. で導出された式は、simple_RNN のコード例で与えられている更新式とは異なるように見えるが、以下のように考えると同じ式が導ける
の更新のケース:
これを今の入れ子のまま計算するのが、更新式1だが.. 各時刻の との積の計算の回数を減らすべく、 と積がとられる の は何なのか? を考えると.. と積を計算すべきなのは、 であるから、
と書き換えられるはずである.
として計算をしてみる
のとき
とする
のとき
のとき
以上から、
講義 p.47 の の漸化式に等しい
以上から以下のようにパラメータが更新できる (simple RNN に書かれた方法と同じ)
順伝播の計算を行う (各時刻の を保存しておく)
から まで順々に下記を実行
最初の時刻まで計算したら勾配法で更新
の更新も 同様の を用いて更新が行える
の更新は 時間方向に遡る必要がないので、更新式の導出その1と同じでOK
実装演習 simple RNN (バイナリ加算)
import sys
sys.path.append('./data')import numpy as np
from common import functions
import matplotlib.pyplot as plt
def d_tanh(x):
return 1-np.tanh(x)**2
def learn_simple_rnn(hidden_layer_size=16, learning_rate=0.1, weight_init_std=1, initializer='Normal', activation='sigmoid', iters_num=10000):
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
input_layer_size = 2
output_layer_size = 1
plot_interval = 100
if activation == 'sigmoid':
h_activation = functions.sigmoid
h_activation_d = functions.d_sigmoid
elif activation == 'tanh':
h_activation = np.tanh
h_activation_d = d_tanh
elif activation == 'relu':
h_activation = functions.relu
h_activation_d = functions.d_relu
else:
print('activation is not valid')
if initializer == 'Normal':
# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
elif initializer == 'Xavier':
# Xavier
W_in = np.random.randn(input_layer_size, hidden_layer_size)/np.sqrt(input_layer_size)
W_out = np.random.randn(hidden_layer_size, output_layer_size)/np.sqrt(hidden_layer_size)
W = np.random.randn(hidden_layer_size, hidden_layer_size)/np.sqrt(hidden_layer_size)
elif initializer == 'He':
# He
W_in = np.random.randn(input_layer_size, hidden_layer_size)/np.sqrt(input_layer_size)*np.sqrt(2)
W_out = np.random.randn(hidden_layer_size, output_layer_size)/np.sqrt(hidden_layer_size)*np.sqrt(2)
W = np.random.randn(hidden_layer_size, hidden_layer_size)/np.sqrt(hidden_layer_size)*np.sqrt(2)
else:
print("initializer is not valid!")
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number/2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number/2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 順伝播
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1) # (1, i)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]]) # (1,)
u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W) # (1,i) (i,hidden) + (1, hidden) (hidden,hidden) = (hidden)
z[:,t+1] = h_activation(u[:,t+1]) # = (hidden, )
y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out)) # (1,hidden) * (hidden,0ut) = (1,out)
#誤差
loss = functions.mean_squared_error(dd, y[:,t])
delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t]) # (o,) \otimes (o,) = (o,)
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:,t])
## 誤差逆伝播
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1) # (i,i)
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * h_activation_d(u[:,t+1]) # (1,hidden) (hidden,hidden) + (1,o)(o,hidden) = (hidden,)
# 勾配更新
W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1)) # (hidden,1) (o,1) = (hidden, o)
W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1)) # (hidden, 1) (1, hidden) = ( hidden,hidden )
W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1)) #
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if(i % plot_interval == 0):
all_losses.append(all_loss)
# print("iters:" + str(i))
# print("Loss:" + str(all_loss))
# print("Pred:" + str(out_bin))
# print("True:" + str(d_bin))
out_int = 0
for index,x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
# print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
# print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()隠れ層の数を変えてみる。8層で必要十分?
learn_simple_rnn(hidden_layer_size = 2, iters_num=20000)
learn_simple_rnn(hidden_layer_size = 4, iters_num=20000)
learn_simple_rnn(hidden_layer_size = 8, iters_num=20000)
learn_simple_rnn(hidden_layer_size = 16, iters_num=20000)
learn_simple_rnn(hidden_layer_size = 32, iters_num=20000)
learn_simple_rnn(hidden_layer_size = 64, iters_num=20000)初期化によってもかなり変わる
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=0.1, iters_num=10000)
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=0.5, iters_num=10000)
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=1, iters_num=10000)
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=2, iters_num=10000)
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=5, iters_num=10000)learning rate は 0.1付近~0.5 の間くらい?? 0.01 のときは単に収束が遅いだけではなさそうにもみえる。
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=1, learning_rate=0.01, iters_num=50000)
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=1, learning_rate=0.1, iters_num=20000)
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=1, learning_rate=0.5, iters_num=10000)
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=1, learning_rate=1.0, iters_num=10000)
learn_simple_rnn(hidden_layer_size = 8, weight_init_std=1, learning_rate=2.0, iters_num=10000)activation は sigmoid なので Xavier がよいはずだが、あまり効果なさそう?? むしろ Normalが一番安定しているように見える.
learn_simple_rnn(weight_init_std=1, initializer='Normal', learning_rate=0.2, iters_num=10000)
learn_simple_rnn(initializer='Xavier', learning_rate=0.2, iters_num=10000)
learn_simple_rnn(initializer='He', learning_rate=0.2, iters_num=10000)活性化関数をtanhにしてみると、Normal より Xavier 収束が早くなっていそう。
learn_simple_rnn(activation='tanh', initializer='Normal', learning_rate=0.075, iters_num=10000)
learn_simple_rnn(activation='tanh', initializer='Xavier', learning_rate=0.075, iters_num=10000)活性化関数を relu にかえると。よいときと悪い時とで差が.. 初期化方法が Normal だと ときどき基本的に収束はむずかしそう。 かなりの頻度で、NaN や overflow (これは勾配爆発が原因だろう) が起きる。
learn_simple_rnn(activation='relu', initializer='Normal', learning_rate=0.1, iters_num=20000)learn_simple_rnn(activation='relu', initializer='Normal', learning_rate=0.1, iters_num=20000)---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
ValueError: cannot convert float NaN to integer
The above exception was the direct cause of the following exception:
ValueError Traceback (most recent call last)
<ipython-input-67-6a829eb4e065> in <module>
----> 1 learn_simple_rnn(activation='relu', initializer='Normal', learning_rate=0.1, iters_num=20000)
2
3
<ipython-input-43-3497d874a704> in learn_simple_rnn(hidden_layer_size, learning_rate, weight_init_std, initializer, activation, iters_num)
103 all_loss += loss
104
--> 105 out_bin[binary_dim - t - 1] = np.round(y[:,t])
106
107 ## 誤差逆伝播
ValueError: setting an array element with a sequence.He を つかうと 収束していそうなケースと、失敗してそうなのが半々くらい。 傾向としては、NaN や overflow が観測される数が著しく減った。
learn_simple_rnn(activation='relu', initializer='He', learning_rate=0.1, iters_num=20000)learn_simple_rnn(activation='relu', initializer='He', learning_rate=0.1, iters_num=20000)
Section.2 : LSTM
動画 day 3-1 2:57 ~ 4:14
LSTMのモチベーション
RNNでは 時系列を遡れば遡るほど、勾配消失/爆発の問題が起きやすく長い時系列の学習が困難 -> ネットワーク構造自体を変えてこの問題の解決をしようとするのがLSTM
勾配消失問題 (内容はStage.3の復習なので割愛)
(確認テスト:2-1) シグモイド関数の微分値の最大値は (2) 0.25 である
勾配爆発
誤差逆伝播していくたびに勾配が指数関数的に大きくなる現象
例えば、学習率を変えると結構頻繁に起きるそうだ
演習チャレンジ: 勾配爆発の対策とである, 下記の勾配クリッピングのコードを埋めろ
回答:1 (grad * rate)
注意: 選択肢だと gradient * norm となっているが コードでは grad で変数は定義されている
# 勾配クリッピングのコード
def gradient_clipping(grad, threshold):
"""
grad: gradient
"""
norm = np.linalg.norm(grad)
rate = threshold / norm
if rate < 1:
return (ここを埋める)
return grad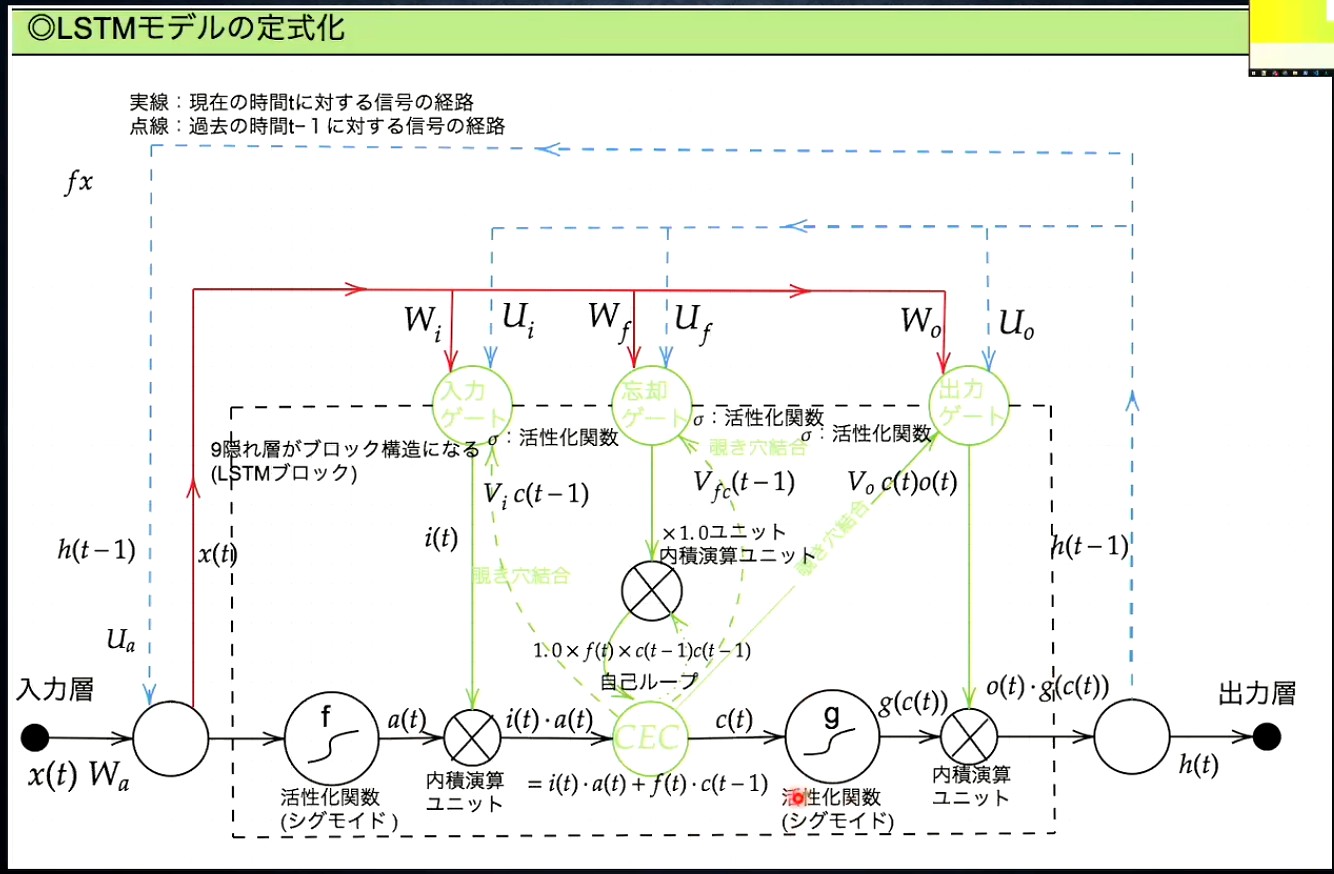
LSTMの全体像:
CEC (constant error carousel)
隠れ層に対する入出力を記憶する機能
構成の着眼点: 勾配が1であれば、時間が遡っても勾配爆発・消失を防げるのでは?
CECからの出力
となるようにする.
満たすべき制約が決まっているので、学習されるパラメータは無い
TODO: 実装するとき何をどうするのか??
入力ゲートと出力ゲート
入力ゲート: CECに何を記憶させるか制御する役割
CECへの入力 と 従来の入力に で重みをかける
を学習する
出力ゲート: CECに記憶された値をどう取り出すかを制御する
隠れ層からの出力 = と で重みをかける
を学習する
忘却ゲート
CECは本来的に過去の情報をすべて記憶しておけるが、情報が不要なときもある。そのときに仕事するゲート
CECからの出力 における で過去の情報をどれだけ使うかコントロールする
を学習する
(確認テスト:2-2) 自然言語を入力して空欄に入る単語を予測する問題をLSTMにとかせるとき、特定の "とても" のように 予測の成否への影響がすくない単語に対してどのゲートが作用するか? -> 回答: 忘却ゲート
講師の説明だと、忘却ゲートでないといけない理由がよくわからないなぁ..
忘却ゲートで の情報をすてるということは、"とても" よりも前の情報も全て捨てることになるので、入力ゲート・出力ゲートのどちらかで扱ったほうがいい問題な気がする?
演習チャレンジ : 空欄は CECの出力を計算する部分なので解答は (3)
覗き穴結合
各種ゲートの入力として、CECの出力 も使ったらもっとうまくいくんじゃないか? という狙いで追加された仕組み
に重み をかけたものを各種ゲートに入力する
実際には大きな効果は得られなかったらしい..
Section.3 : GRU
動画 day 3-1 4:25 ~ 4:48
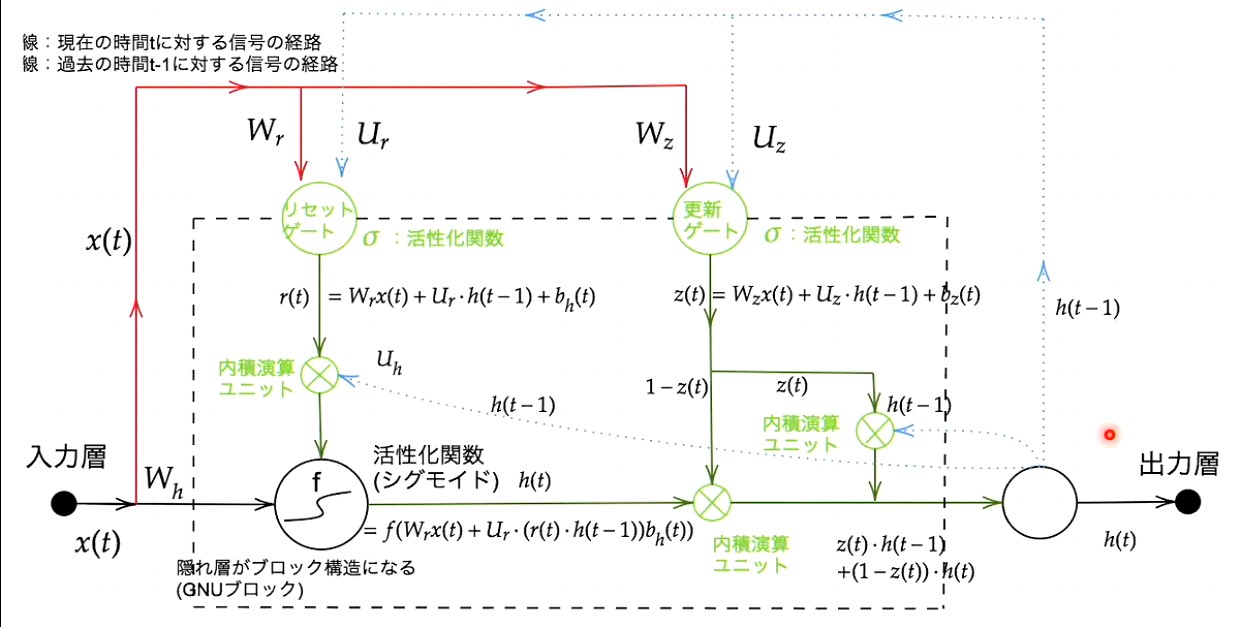
この図は沢山まちがってるので、要注意
の計算には シグモイド関数の適用がされるべき
は間違い。 は隠れ層全体の出力のみ.
リセットゲートの重みと 隠れ層の計算のもともとの重みが混同してる
の計算の段で、 と の使い方が逆
もちろん逆にしてもうまく動くはずだが、その後の演習チャレンジとの矛盾をなくすためには修正すべき
GRUのモチベーション
LSTMはパラメータ数が多く、計算負荷が高い -> 精度はなるべく落とさず、パラメータを大幅に削減
(確認テスト:3-1) LSTM, CEC の課題
LSTM全体の課題は、上述の通りパラメータが多く計算負荷が膨大なこと
特にCECに記憶機能のみを分離したことでブロック構成が複雑になる要因となった
(確認テスト:3-2) LSTMとGRUの違い:
LSTM よりも GRU の方が パラメータが少なく、計算量が少ない
DLの研究はそういう流れが多い
GRUの概要
CECがなくなり隠れ層の に過去の情報が保存される
リセットゲート
の更新式において、 が にかかることで、過去の情報をどういう重みで使用するかがきまる?
とはいっても、 は現在時刻にもかかっていて、独立ではないんだな
忘却ゲートみたいなもの?
更新ゲート
出力ゲートみたいなもの
演習チャレンジ : gruの順伝播のコード
回答: もとめられているのは、隠れ層の出力を計算するコードなので (4) (1-z) h + z h_bar
ソースコード "predict_word.ipynb" の実行について
動画講義では、"Tensorflow 1.x を指定して各セルを実行すれば、学習が実行される" と言われていたが、学習済みモデルをloadして、予測(推論)が一つ実行されるだけである
build_dic(), train() の実行はコメントアウトされ実行されない
試しにコメントアウトを外してみたが、build_dic()は 実行できたものの、train() は下記のエラーが発生して実行できなかった.
ValueError: Variable rnn/basic_rnn_cell/kernel already exists, disallowed. Did you mean to set reuse=True or reuse=tf.AUTO_REUSE in VarScope? Originally defined at (以下略)- メンテされているかどうかもわからないので、今回この問題は放置してここでは、推論, 予測の関数だけ見ておく.
def inference(self, input_data, initial_state):
"""
:param input_data: (batch_size, chunk_size, vocabulary_size) 次元のテンソル
:param initial_state: (batch_size, hidden_layer_size) 次元の行列
:return:
"""
# 重みとバイアスの初期化
hidden_w = tf.Variable(tf.truncated_normal([self.input_layer_size, self.hidden_layer_size], stddev=0.01))
hidden_b = tf.Variable(tf.ones([self.hidden_layer_size]))
output_w = tf.Variable(tf.truncated_normal([self.hidden_layer_size, self.output_layer_size], stddev=0.01))
output_b = tf.Variable(tf.ones([self.output_layer_size]))
# BasicLSTMCell, BasicRNNCell は (batch_size, hidden_layer_size) が chunk_size 数ぶんつながったリストを入力とする。
# 現時点での入力データは (batch_size, chunk_size, input_layer_size) という3次元のテンソルなので
# tf.transpose や tf.reshape などを駆使してテンソルのサイズを調整する。
input_data = tf.transpose(input_data, [1, 0, 2]) # 転置。(chunk_size, batch_size, vocabulary_size)
input_data = tf.reshape(input_data, [-1, self.input_layer_size]) # 変形。(chunk_size * batch_size, input_layer_size)
input_data = tf.matmul(input_data, hidden_w) + hidden_b # 重みWとバイアスBを適用。 (chunk_size, batch_size, hidden_layer_size)
input_data = tf.split(input_data, self.chunk_size, 0) # リストに分割。chunk_size * (batch_size, hidden_layer_size)
# RNN のセルを定義する。RNN Cell の他に LSTM のセルや GRU のセルなどが利用できる。
cell = tf.nn.rnn_cell.BasicRNNCell(self.hidden_layer_size)
outputs, states = tf.nn.static_rnn(cell, input_data, initial_state=initial_state)
# 最後に隠れ層から出力層につながる重みとバイアスを処理する
# 最終的に softmax 関数で処理し、確率として解釈される。
# softmax 関数はこの関数の外で定義する。
output = tf.matmul(outputs[-1], output_w) + output_b
return output
def predict(self, seq):
"""
文章を入力したときに次に来る単語を予測する
:param seq: 予測したい単語の直前の文字列。chunk_size 以上の単語数が必要。
:return:
"""
# 最初に復元したい変数をすべて定義してしまいます
tf.reset_default_graph()
input_data = tf.placeholder("float", [None, self.chunk_size, self.input_layer_size])
initial_state = tf.placeholder("float", [None, self.hidden_layer_size])
prediction = tf.nn.softmax(self.inference(input_data, initial_state))
predicted_labels = tf.argmax(prediction, 1)
# 入力データの作成
# seq を one-hot 表現に変換する。
words = [word for word in seq.split() if not word.startswith("-")]
x = np.zeros([1, self.chunk_size, self.input_layer_size])
for i in range(self.chunk_size):
word = seq[len(words) - self.chunk_size + i]
index = self.dictionary.get(word, self.dictionary[self.unknown_word_symbol])
x[0][i][index] = 1
feed_dict = {
input_data: x, # (1, chunk_size, vocabulary_size)
initial_state: np.zeros([1, self.hidden_layer_size])
}
# tf.Session()を用意
with tf.Session() as sess:
# 保存したモデルをロードする。ロード前にすべての変数を用意しておく必要がある。
saver = tf.train.Saver()
saver.restore(sess, self.model_filename)
# ロードしたモデルを使って予測結果を計算
u, v = sess.run([prediction, predicted_labels], feed_dict=feed_dict)
keys = list(self.dictionary.keys())
# コンソールに文字ごとの確率を表示
for i in range(self.vocabulary_size):
c = self.unknown_word_symbol if i == (self.vocabulary_size - 1) else keys[i]
print(c, ":", u[0][i])
print("Prediction:", seq + " " + ("<???>" if v[0] == (self.vocabulary_size - 1) else keys[v[0]]))
return u[0]Section.4 : 双方向RNN
動画 day 3-1 4:48 ~ 4:57
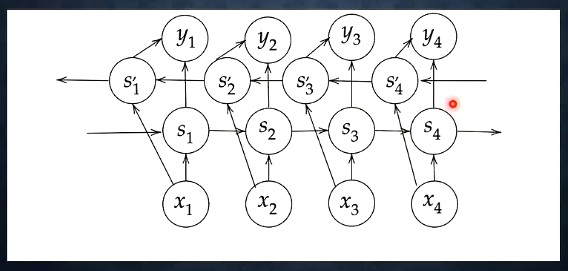
過去の情報だけでなく、未来の情報も加味することで精度を向上させるモデル
通常のRNN における過去の情報を活かす隠れ層 を時間方向に逆転させた隠れ層 が追加される
自然言語処理等においても、文意を理解するときには前後の情報を使うのが自然。RNNの拡張としては自然な形.
演習チャレンジ: 双方向RNNにおける出力層の計算として正しいものは?
(4) '''np.concatenate([hf, hb[::-1]],axis=1)''' がうまる.
理由: 問題の箇所の次の行で、得られた配列と、行列V (outputsize, 2*hiddensize) との行列積をとっている. ここから、時間方向の連結ではなく、特徴量方向の連結であることがあきらか。
zip で取り出してきた hf,hb が二次元以上の配列になっていないと、axis=1に対するconcatinate はエラーが出るはずなので、hsf, hsb がもともと三次元の配列でないといけないのだが、それはコードからは明確には読み取れない.
Section.5 : Seq2Seq
動画 day 3-1 4:57 ~ 5:45
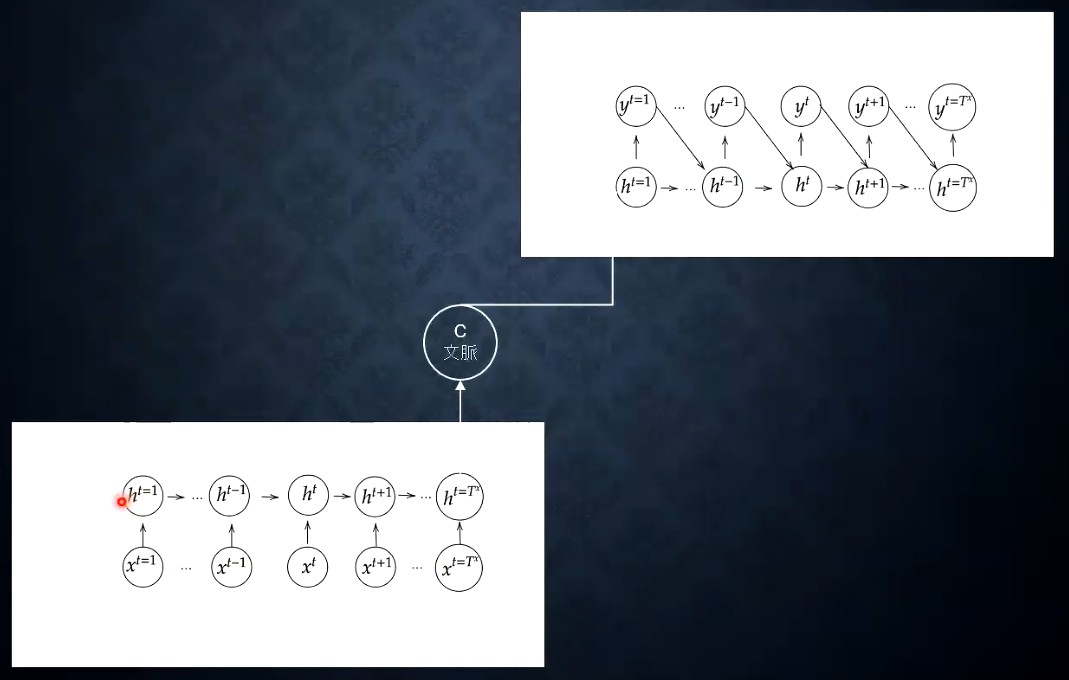
seq2seq の全体像
時系列の入力から、時系列の出力を得る
機械翻訳、対話システムなどの応用例がある
ざっくり構成
Encoder (下側のネットワーク) で 文章から文脈を抽出
Decoder (上川のネットワーク) で 出力を変換 (例えば同じ意味の別言語の文章)
Encoder, Decoder は 必ずしもRNNでなくてもよく、LSTM, GRUなど時系列を扱えるモデルであれば構わない
基本的な seq2seq の構成
Embedding
近い意味の単語ほど距離が近く配置されるような特徴量(ベクトル)表現
経験的には数百次元程度
自然言語処理では、数万語彙程度を想定するが、これをonehotベクトルのまま扱うのはあまりに次元数が大きすぎる
かといって、単語IDそのままではうまく処理ができない (分類問題をonehotエンコーディングするのと同じ理由)
MLM (Masked Language Model) を使用したEmbedding 学習の例
既存の文章から単語を一つマスクして、マスクされた単語の当てっこ問題を解かせる。その過程でEmbedding 表現が自然と学習されていくという手法
学習に使用する問題を既存の文章からいくらでも生成でき、人手でラベルを降る必要がない点で優れている
複雑なモデルを学習させたり、性能をあげたりしやすい
Encoder RNN
文意 (thought vector) を得る役割を持つ
入力: 文を構成する単語ひとつひとつをベクトル表現したもの
単語ID -> embedding 表現 (後述)への変換する
処理: 1語(に対応する1ベクトル)ずつ入力して隠れ層を更新していく
出力: 文の単語を順番に全て入力し終わったときの隠れ層のベクトルが thought vector となる
Decoder RNN
翻訳結果や、対話文などの単語を一つずつ生成する役割を持つ
処理内容:
Encoder RNN の final state = thought vector を Decoder RNN の隠れ層の initial state として設定
Decoder 側の に Encoder 側の を代入, ということ
2サンプルめ以降の Decoder RNN への入力 は、1サンプル前で得られた単語のEmbedding 表現
どのように単語を得るか??
Decoder RNN の出力 Embedding を onehot ベクトルへの逆変換
onehot ベクトルが、各トークンの生成確率を表すので、これをもとにランダムサンプリング(単語IDが確定)
サンプリングされた単語IDに対応する onehotベクトルを再度 Embedding 表現に変換 -> 次のサンプルの 入力として使用
トークン(単語ID) か文字列になおして文章を得る (Detokeninze)
(確認テスト:5-1) seq2seq の説明として正しいものは.. (2) 「RNNを用いたEncoder-Decoder モデルの一種であり、機械翻訳などのモデルに使われる。」
は双方向RNN, 3. 構文木, 4. はLSTM自体の説明であり、これらを使うことは seq2seq の必須要件にはなっていないので不適切
演習チャレンジ: onehot ベクトル w から、embedding 表現 e を取得するコードは (1) E.dot(w) である.
E のサイズが (embedsize, vocabsize) となっていることから、行列積として次元の辻褄があるのは (1)
seq2seq の拡張
HRED
文章(複数の文)の文脈を考慮した応答・翻訳などを行うための工夫
Encoder/Decoder の間に、各文の文意を context hiddent state として保持し、RNNで更新する層 = Context RNN を追加
課題:
例えば対話システムなどでは、短く・情報量に乏しい返答が 良い返答であると学習しがち
いろいろな文脈に対して、そうしたありがちな回答がもっとも確率が高くなるため
応答のバリエーションを増やすには 何か追加で工夫が必要
VHRED
上記 HREDの課題を解決して、バリエーションに富んだ応答ができるようにしたもの
後述のVAEにおける潜在変数のアイディアを HREDに導入
(確認テスト:5-3)
seq2seq は 時系列データを入力して別の時系列データを出力するネットワーク
HRED は seq2seq に context を扱う機構を追加することで、文脈を考慮した出力をえられるようにした手法
VHRED は、HRED が 当たり障りのない出力しか得られないという課題を、VAEの考え方を取り入れて解決した手法
VAE (Variational Autoencoder )
普通のオートエンコーダー
入力 -> (エンコーダー) - > 潜在変数 -> (デコーダー) -> 出力
入出力が同じ(なるべく近く)なるように、エンコーダー・デコーダーを学習する
潜在変数の次元を、もとの入出力の次元よりも小さく設定することで、情報の圧縮・進捗を行うNNを学習する
どのような圧縮が行われるかは全くわからない
VAE
オートエンコーダーの潜在変数に 標準正規分布を仮定する
狙い: 潜在変数で表される特徴量空間において、似たデータが近い位置に配置されるようになる
学習方法: エンコード時に、潜在変数にあえてノイズを加えることで
まったく同じデータをいれても、ノイズによって少しずれたデータが、デコーダーに入力される
このような状態でデータをうまく復元しやすくするには、似たデータが近くにあったほうがよく、そのように学習が行われる
(確認テスト:5-2) VAEは、AE(自己符号化器)の潜在変数に "確率分布" を導入したものである
Section.6 : Word2vec
動画 day 3-1 5:45 ~ + day 3-2 0:00 ~ 1:54
ざっくり概要: 単語をベクトル表現する手法
単語の onehot ベクトルから、Embedding 表現をえる手法の一つ
onehot ベクトルと W の積によって、Embedding 表現が得られるように、(onehot ベクトルの次元数) x (embedding 表現の次元) のサイズの重み行列 W を学習
実際には テーブル引きになる (onehotベクトルの積は行または列の取り出しになるため)
これにより、大規模データの分散表現の学習が現実的な計算速度とメモリで実現できるようになった
Section.7 : Attention Mechanism
動画 day 3-2 1:54 ~
Attention Meachanism のモチベーション
seq2seq の隠れ層は固定次元のベクトルであり、入力が長文である場合にその文意を表現することが難しくなってくる
着眼: 文中の重要な単語・互いに関連の強い単語がどこかを見極めることができれば、長文であっても限られた次元でのベクトルで文意を表せるのでないか? -> Attention Mechanism
近年(講義動画作成の2019年時点)で、精度の高い自然言語処理モデルはどれも、Attention Mechanism Wo使っている、とのこと
(確認テスト:7-1)
RNNは時系列データを処理するのに適したネットワークであり、
word2vec は 単語の分散表現を得るための手法
seq2seq はある時系列データから別の時系列データを得るネットワーク
Attention は 時系列データのそれぞれの関連性に重みをつける手法
Day.4
Section.1 : 強化学習
強化学習とは?
行動の結果として得られる利益をもとに、行動選択の原理を習得してく機械学習の一分野
機械学習を大きく3種類に分けると 教師あり学習・教師なし学習・強化学習
教師あり, 教師なし学習が 一問一答形式のタスク(とその延長線上にあるタスク)を扱い、データに含まれるパターン(問題をよくためのよい特徴量)を見つけることがキモになっていた
強化学習は、問題にたいして優れた方策を見つけることが目標
昔からあったが、計算資源が豊富になったこと、ブレークスルーとなる手法がうまれたことから、最近特に注目をあつめるようになった
強化学習のざっくりイメージ
環境: 問題が定義された場
エージェントの行動に対して、報酬、状態Sに起因する観測を返す
例: 会社の販売促進部
報酬を返す : キャンペーンを打ったことによる負の報酬 + キャンペーンの効果で得られる売上という正の報酬
観測: (動画では語られてないが) 誰が何買ったなどの情報?
エージェント: 強化学習の主人公
環境から得られた報酬と観測から、価値 V と 方策 π を更新(学習)しながら、次に取るべき行動を(方策を元に)選択する
例: 顧客のプロフィールと購入履歴に基づいて、キャンペーンメールを送る顧客を決めるソフトウェア
行動: 顧客ごとにメールの送信・非送信を決める
(予想されるベターな)方策: キャンペーン商品のみを購入するコスパの悪い客は非送信、キャンペーン商品のついでに他の利ざやのある商品も購入してくれる客には送信
価値: (動画では語られてないが) キャンペーン終了時点での報酬合計の予測値?
実際に機械学習で動かす場合には..
はじめから報酬が得られる方策を選び取れるような知識を持たない
最初は当てずっぽうで行動を決め、徐々に何をしたら報酬が得られるか情報がたまってきたら報酬を得やすい行動を選ぶ
探索(未知の行動をとって新しい情報を得る) と 利用(過去の情報からベストな行動をとる)はトレードオフ
過去のデータからベストとされる行動のみを取り続けると、よりよい行動があることにきづけない
未知の行動のみ取り続けると、トータルで報酬が少なくなってしまいかねない
何を学習するか?
方策(方策関数 )
価値( 主に行動価値関数 )
(方策ベースの?) Q学習の概要
価値関数
この調子で(いまの方策に従って)続けたら、最終的な報酬がどれくらいになるか? を計算したもの
状態価値関数 : 状態 のみによって決まる
行動価値関数 : 状態 と 行動 の両方に依存
最近良く使われるのはコチラ
方策関数
その時々の状態でどのような行動をとるとベストかを求めるための確率を与える関数
(方策ベースの手法の?) 解き方
"最大化" すべき 期待収益(報酬) を として勾配法で 方策関数を のパラメータを最適化
は 方策勾配原理によって下記で得られる
ん? 関数はどうやって更新するんだ? -> AlphaGoの例からよみとってみよう
Section.2 : AlphaGo
Alpha Go Lee
Policy Net (方策関数) :
入力: 盤面 19x19 x 48ch
1~3ch : 自分の石, 的の石, 空白
4ch~ : その他の情報
着手履歴として 1手前, 2手前,.., 8手前に打たれた石 (8ch)
それぞれの位置に石を打つとシチョウで取れるor取られるか (2ch)
合法手であるかどうか (1ch) etc...
出力: 盤面 19x19 それぞれの場所がベストの手である確率
ネットワーク構造
入力-> 5x5 conv 192ch -> relu
(3x3 conv 192ch -> relu ) x 11回
1x1 conv 1ch -> softmax -> 出力
Value Net (行動価値関数) :
入力: 盤面 19x19x49ch
Policy Net の入力 + 今自分の手番が黒番であるかどうか?
出力: スカラー (勝利確率 -1~+1)
ネットワーク構造
殆どPolicyNet と同じで、最後全結合層で 1x1 に変換
ネットワーク構造の選び方について
盤面の情報が2次元なので、基本的にはconvnet だと講師の方は強調していた
学習の概要
強化学習をうまくまわすための工夫
RollOutPolicy
より軽量な 線形の方策関数をつくっておき, ValueNetの強化学習中に PolicyNet の代わりとして使うことで 学習のループを高速化する
人手で選んだ特徴量を用いる
PolicyNetの演算時間 3ms に対して こちらのモデルは マイクロsecオーダー
PolicyNet の教師あり学習
ネット囲碁の棋譜データ(人間の手) を教師として次の一手を予測
PolicyNet は 精度 57% だったらしい
PolicyNet の強化学習
PolicyPool に色々なPolicyNetを格納しておき、現在のPolicyNet と Poolからランダムに選択肢Policy Net で対局させながら学習を行う
ValueNet の強化学習
PolicyNet どうしの対極シミュレーションを教師として学習
途中経過の盤面を入力して、対局結果を予測する
"モンテカルロ木探索"という手法を用いて パラメータを更新
ここで使うPolicy として RollOutPolicy で代用
Alpha Go Zero
教師あり学習を使わない
入力を盤面情報のみにした
Alpha Go Lee では、石の配置のみでヒューリスティックな特徴入力を廃した
PolicyNet + ValueNet を一つのネットワークに統合
前半部がおなじ形状をしていたので、(パラメータ共有ができることを期待して?) 1つに統合
入力: 19x19 17ch
17ch はなんだろう??
出力: Policy出力と、Value出力
ネットワーク構造
共通パス: 入力 -> conv 3x3 256ch -> BN -> Relu -> Residual Block x 39
Policy パス : 共通パス -> conv 1x1 2ch -> BN -> ReLU -> fc 362 -> softmax -> 出力
Value パス : 共通パス -> conv 1x1 1ch -> BN -> ReLU -> fc 256 -> ReLU Fc1 -> tanh -> 出力
Residual Network の導入
Residual Net とは?
ネットワークにショートカット構造を追加して、勾配の爆発・消失を防ぐ
Residual Block の基本形:
入力-> conv -> BN -> ReLU -> conv -> BN -> 入力をここに足す -> ReLU
解釈:
Residual Block は、skipt と conv の2つの入力の足し算
Residual Block が N 個あったら それぞれのblock で skip or convをどちらを選択したかで 種類の経路がある
これは 個のネットワークのアンサンブル出力を得るような効果があるのではないか?
Alpha Go Zero での Residual Block 使い方の工夫
ResidualBlockの構造自体の工夫
Bottleneck : 2層相当の計算量で、3層にする (非線形を増やす)ため、1x1 conv で次元削減してから、3層目で次元復元
PreActivation: オリジナルとは異なる並びにした(Activationの位置を変えた)
Network 全体の工夫
WideResNet : convフィルタ数をk倍に増やして、浅い層数でも精度をあげる、GPUを効率的に使って学習早くまわす
PyramidNet: いきなり幅を増やすとその直後の層に負担?がかかるので、徐々に1層ずつふやしていく
講師のコメント: E資格の問題では "○○の手法ではどういう工夫がされたか?" みたいな問題がよく出される
基本的な要素を組み合わせ方を変えたものに、名前がついているだけなので、そんなに大したことじゃない場合も多いが、試験対策にはなる
現在のDLの基本的な要素は、畳込み, pooling, rnn, attention で、あとはこれらを組み合わせているだけ
モンテカルロ探索時の RollOutやめた
自己対局によって Value出力 の教師をつくる点は一緒
学習前後のネットワークで、対局テストを行い学習後ネットワークの勝率が高ければ更新する
Section.3 : 軽量化・高速化技術
実際にDNNのアプリケーションを開発するときに必要な実践的な知識
いかにモデルを早く学習するか? (高速化技術)
Intro
CPUの性能向上は 18~24ヶ月で2倍程度(ムーアの法則)、それに対してDLは1年で10倍複雑になっている
手段1: 分散深層学習(複数のコンピュータを使ってモデルを学習する) で対応
端末数を複数にすることはもちろん、CPU, GPU, TPUなどの演算ユニットを複数にすることなども含む
最近では世界中に散らばったスマートフォンのリソースを使うなどもある
手段2: 深層学習ユースケースに対して性能がCPUよりも高い 演算ユニットを用いる
まぁ、これも内部的には、演算器の並列化をしているけれども..
データ並列による分散学習
モデルを各ワーカーにコピーし、データを手分けして処理する
モデル並列に比べると同期タイミングを減らせるため、複数端末間での並列化で使われることが多い
同期型
各ワーカーの勾配計算が終わるのを待ち、全ワーカーの勾配の平均を用いて親モデルのパラメータを更新する
更新された親モデルを各ワーカーにコピー
非同期型
各ワーカーはお互いの勾配計算を待たず、各子モデルごとにパラメータを更新する
各ワーカーは、"パラメータサーバ" にモデルを Push
各ワーカーが 新たに学習を始めるときには、パラメータサーバから Pop したモデルを使う
各方式の比較
処理のスピードは非同期型の方が早い
1イタレーションあたりの精度向上という点で、同期型の方が安定した効果が得られる
(どちらも可能なケースでは) 同期型が使われることが多い
モデル並列による分散学習
親モデルを各ワーカーに分割し、それぞれのモデルを学習させ、全てのモデルの更新が終わったら親モデルを更新
モデルの分割方法は様々だが、カスケードにつながった層を分割するよりは、分岐したところを分割するケースの方が多い
ワーカー間の同期の頻度が大きいため、同一コンピュータ内での複数演算ユニット間の並列化で使われる
参照論文: Large scale Distributed Deep Networks
2016年のGoogleの論文, Tensorflowの元となったアイディア
GPUによる高速化
原理
CPU: 高クロックで複雑(汎用) の演算を行う。
GPU: 比較的低クロックで、簡単な演算に特化しているが、大量のコアによる並列処理を前提に作られている
深層学習の 大半の演算は、行列演算など GPUでサポートされているおきまりの演算の組み合わせ
性能 x コア数のトータル性能でみると、GPUの方がはるかに高速に処理できる
GPGPU開発環境
CUDA
NVIDIA社製GPU専用の GPGPU向けSDK
DeepLearning 専用APIも提供されており使いやすい
OpenCL
NVIDIA社以外のGPUからでも使用可能な GPGPU向けSDK
DeepLearning 専用というわけではない
現在の状況
Tensorflow, Pytorch などの DeepLearning フレームワークは、上記のSDKをラップしており、モデル開発社が直接 CUDA/OpenCLを触ることはない
現状は CUDAがデファクトで、OpenCLをDeepLearning に使うことはまれ
以下に推論を軽量に行うか? (軽量化技術)
量子化 (Quantization)
量子化では、(ネットワーク構造自体は変えずに) パラメータ1つあたりが専有するメモリ量を減らすことを考える
64bit 浮動小数点数 -> 32bit, 16bit の浮動小数点など
DeepLearning におけるメモリと演算量は基本的にモデルのサイズ=パラメータの数で議論するようだ
例:
BERTという自然言語処理のモデルは、一番小さいものでも、10億個程度のパラメータがあり、300~600MB
これはスマートフォン上での実行メモリとしては大きいので小さくしたい
1word あたりの使用メモリを 8 byte -> 4byte -> 2cyte などにできれば メモリ量は、1/2, 1/4 にできる!
浮動小数点数については既知の内容のため割愛
メモリ量低減以外の効果(メリット/デメリット)
計算の高速化
倍精度演算(64bit) と 単精度演算(32bit)の性能が異なる
GPU (Tesla 系) では、大体精度に反比例
現在最新の Tesla A100 ならば 半精度演算(16bit)をサポートしており 150TFLOPS !
演算精度の低下具合
画像系なら 半精度演算で精度の問題ないケースが多い
更に量子化で減らした研究例: 物体検出での 32bit -> 6 bit
演算時間 約1/5~1/4程度(期待通り)
mAP で 0.5% 程度の精度差 (BBの余白が微妙に大きいかな?程度) で実使用上問題なし
仮数部と指数部のbit 割当を変えた特殊は浮動小数点表現を使うこともあるので、注意
蒸留
学習済みの複雑,高精度なモデル(教師モデル)を頼りに 同程度の精度のより軽量なモデル(生徒モデル)をつくる
生徒モデルのネットワーク構造自体は、教師モデルよりシンプルなものになる
手法イメージ
通常の学習では、学習データとして、あらかじめ用意された入出力のペアを使うが、蒸留では 正解ラベルのの代わりに教師モデルからの出力を使う(ということだと解釈した)
予想される利点 (特に動画では解説されていない)
入力さえ用意すれば、人手でラベルをつけずとも大量の学習データを用意できる
教師モデルからの出力には、理想的なラベルと比べて豊富な情報が含まれる
例えば、画像分類のケースだと、人手でつけたラベルは各次元 0 or 1 の理想的な出力だが、蒸留においては 教師モデルからの出力は各次元0~1の間の値をとり、そこには どのクラスとどのクラスが画像として似た特徴量を有しているか? という情報が含まれる。
例えば、雑音抑圧のようなケースだと、通常の学習では、完全にクリーンな出力との誤差を最小化しようとするが、蒸留において、教師モデルからの出力には多少のノイズは残留しており、そこには、大きなモデルでも消せなかったノイズ成分はどのようなものか? 教師モデルが雑音抑圧性能 vs 画質 のバランスを慎重にチューニングして得られたモデルであるならば、そのバランシングの情報もそこに含まれることになる。
注意: 少し調べた所によると、教師モデル出力との誤差を、soft loss ラベルとの誤差を hard loss と予備その両者の和を最小化するような学習をする、という情報が出てきた
蒸留の効果
cf. FITNETS: HINTS FOR THIN DEEP NETS
cifar10 タスクに対して、層数5 (ネットワーク構造不明) の軽量なモデルを学習させたとき
ゼロベース: 83.5% 強
蒸留 : 84.5% 弱
プルーニング
ネットワークが大きい場合、必ずしもすべてのニューロンが出力に大きく寄与しない -> 寄与の小さいニューロンを削除してモデルの複雑さを低減する
手法イメージ
学習中に 重みが閾値以下になったニューロンは削除する
? 削除というのは実装としてはどのようにやるんだろう??
プルーニングの効果・実例
oxforrd102 category owner dataset を CaffeNet で学習したあと、プルーニングをやってみた
しきい値を0.5 とした場合: 48.86 % のパラメータが消えて、精度 91.66 %
しきい値を1.5 とした場合: 94.18 % のパラメータが消えて、精度 90.69 %
Section.4 : 応用モデル
具体的なモデル各論
特にE資格頻出のもの
覚えていれば即答できる
ここで扱われているもの以外も、シラバスにかかれているものは要チェック!
MobileNets: Efficient Convolution Neural Networks for Mobile Vision Application
"精度を維持した軽量化・高速化" を行った画像認識モデル
画像認識モデルは2017年までに完成( 精度は実用レベルに向上)
軽量化のための特徴的な手法
注意: 以下、Convolution の演算量は、積の数のみカウント(和は無視) している
通常のConvolution
空間方向の畳み込みと、チャンネル方向の計算を(最大の自由度で)一度に行う
仕様
入力: H x W x C
カーネル: K x K x C (フィルタ数 M)
出力: H x W x M
ストライド1, padding 1
演算量: H x W x ( K x K x C x M)
MobileNets で用いる 特殊な Convolution
以下の Depthwise Convと、 PointwiseConv 縦列につなげて、パラメータ数と演算量を減らしながら、通常のConvと似た効果を得ることを狙う
Depthwise Convolution
空間方向の畳み込みを行うが、チャンネル間計算を行わない
各入力チャンネルに共通のフィルタを畳み込んでそれぞれを出力とする
資料に "各層毎の畳み込み" と書かれているのは typo だと思われる
入力: H x W x C
カーネル: K x K x 1 (フィルタ数は1)
出力: H x W x C
演算量は H x W x ( C x K x K)
Pointwise Convolution (1x1 conv)
チャンネル間計算を行うが、フィルタが1x1の
入力の各点毎の演算, つまり各チャンネルの同位置のピクセルの線形結合を出力とする
入力: H x W x C
カーネル: 1 x 1 x C (フィルタ数 M)
出力: H x W x M
演算量は H x W x (C x M)
最終的な演算量
H x W x ( C x K x K) + H x W x (C x M) = H x W x ( C x ( K x K + M) )
通常のconに対して (K x K + M) / (K x K x M) 倍
メモリも軽くて、VGGNets 300 ~ 600 MB に対して MobileNet は 14M
現在 MobileNets は第三世代まで開発されているらしい
DenseNet : Densely Connected Convolutional Networks
CNNアーキテクチャの一種. 層を重ねた際の勾配消失問題の解決をモチベーションとするのは ResNet と同じだが、解決の方法がことなる.
アーキテクチャ 概要
概要
input -> conv
-> ( Dense Block -> conv -> pool ) x 2
-> Dense Block -> pooling -> Linear -> output
特徴的な層の説明
Dense ブロック
出力層に前の層の入力層を結合する計算を何度か行う
DenseBlock内 L層目の出力を とすると
, 出力チャンネル数は チャンネル
は BN -> Relu -> 3x3 conv のような形
を grohth rate と呼ぶ
- ResNet との違い - ResidualBlock の中の skip connedction は一つだけ, DenseBlockは各層毎 - ResNetでは skipされたものがAddされる. DenseNet は連結
Transition Layer
Dense ブロック 直後の conv -> pool の部分
Dense ブロックで膨れ上がったチャンネル数を減らす(conv の出力チャンネル数で絞る)
Batch Normalization の問題点と その他の Normalization
Batch Normalization
レイヤー間の流れるデータの分布をミニバッチ単位で正規化する -> ピクセル,チャンネル毎に サンプル方向の正規化
学習時間の短縮や初期値への依存低減、過学習の抑制などの効果がある
問題点: バッチサイズが小さいときには、学習は収束しないことがある
GPUのメモリ量の制約などで、バッチサイズを変えざるをえない
実行する端末によって、条件を変えなければいけないバッチサイズに依存する BNはできたら避けたい
その他の Normalization
Layer Normalizatrion
それぞれのサンプル毎に、ピクセルandチャンネルに対する正規化
バッチサイズ依存の問題は解決できる
理論上バッチサイズとやってることは全くことなるが..
入力のスケール, 重み行列のスケール・シフトに関してロバスト
Instance Normalization
それぞれのサンプル、それぞれのチャンネルごとに, 全ピクセルの正規化
バッチサイズが1の場合と等価
コントラスト正規化・画像のスタイル転送・テクスチャ合成のタスクで使用例あり
Wavenet
音声の生成モデルとして提案された、時系列データに対して Dilated Convolution を適用する
Dilated Causal Convolution が導入された
層が深くなるにつれて入力データを飛び飛びにすることで受容野を増やす
因果性(causality)
Section.5 : Transformer
"Transformer 以前" 的な位置づけで RNNによる seq2seq をまずは取り上げる
RNN による 言語モデル
RNN については day3 参照
ここでは、時系列情報を固定長の内部状態に変換できるものと捉える
言語モデル
単語の並びに対して尤度を評価できるもの
つまり、時刻 t-1 までの情報で時刻 t の事後確率を求められれば、言語モデルができる -> RNN使える
RNN x 言語モデル
言語モデルを再現するようにRNNの重みが学習されれば、
各時刻で次にどの単語が来るのが自然かを確率分布として出力でき
Argmax で次の単語を予測できるので
先頭単語を与えれば文章生成が可能
seq2seq = (RNN を用いた) Encoder - Decoder モデル
Encoder で 入力系列を内部状態へ Decoder で、内部状態を出力系列へ
Decoder 側の 内部状態初期値 として Encoder の内部状態が渡されていることが鍵!!
Encoder 側は なにかしら適当な初期値が与えられている
Decoder の output 側に正解を与えれば教師あり学習が End2Endで行える
seq2seq コード説明 メモ
データセットから単語辞書を作る
今回しようしたのは タナカコーパス
データセットに含まれる単語のうち登場回数が2回以上の単語を辞書煮含める
特殊トークンも追加
<PAD> : バッチ処理の際に系列の長さをそろえるために、短い系列の末尾をうめるためのトークン
<BOS>, <EOS>: センテンスのはじめ、おわり
<UNK> : 未知(学習時に使用したボキャブラリーに含まれない)の単語
単語列を単語のID列に変換し、DataLoader を作成
DataLoader は ミニバッチデータを用意するイテレータ
next 関数に
バッチを取得し
入力系列の末尾にパディングし
テンソルに変換して転置
転置は 後述する PackedSequence に食わせるため
(次の処理のために)ポインタを更新
モデルの構築
導入: PackedSequence
PyTorch では 可変長系列(パディングした部分)の処理を効率的に行えるような形式に系列を変換するPackedSequence というクラスがある。
RNN入力前に packpaddedsequence() 関数で変換
RNN出力を padpackedsequence() 関数で逆変換して、pad済みテンソルに戻る
Encoder: Embedding -> pack -> gru -> pad
Decoder: Embedding -> gru
Decoder の 入力は padding してないので、pace/pad の変換は不要
Encoder と Decoder をくっつける
decoder の入力と隠れ状態の初期状態を定義
decoder 出力を受ける変数を定義
for 文で時刻毎に処理
Teacher Forcing
Decoderは本来 時刻t-1の出力を 時刻tの入力するものだが、正解ラベルを直接Decoder の入力にすること
sequence のはじめで間違えるとその後ろの学習で誤差がどんどん拡大して学習がうまくまわらない問題への対策
とはいえ、推論時は自分自身を入力して動作させるものなので、毎回正解ラベル入れるのも不適切
そのため確率的にTeacher Forcing を実行
訓練
BLEU : 翻訳の精度を評価するための指標
小さいコーパスなので、精度は高くないが、いくつかの入力に対してはうまく翻訳できることもある
Transformer の説明
Attention (注意機構)(Bahdnau et.al., 2015)
モチベーション: 長い文章への対応
上記説明した(RNNベースの)seq2seq の弱点 = 長さに弱い
長い文章の情報を 固定長ベクトルに押し込めることが難しくなってくる
翻訳先単語毎に予測時に特に注意を向けるべき入力単語を絞る
Source Target Attention
翻訳元の各単語の隠れ状態の加重平均 を活用
翻訳先の各単語を選択するときに、翻訳元のどの情報に注目すべきか? の情報を与える
ここでは、Scaled Dot Product Attention を前提とする
モデルの次元数 でスケーリングする
例: 英仏翻訳
固有名詞や数字などは、1対1対応している
単語間の逐語訳ができない状況では、複数の単語に対して重みがあらわれる
Attention は ざっくり 辞書オブジェクトとみなせる
翻訳先単語を Query として, 対応する翻訳元単語 Key を見つけて Value を取り出す操作
実際には重み付け平均なので,,
翻訳先単語 (Q:query) のベクトルと 翻訳元単語(K:key)との類似度をはかり、
類似度を softmax で 足したら1となるような重みに変換
Valueと積をとって重み付け平均していることになる
- 効果: 入力文が長くなっても精度が落ちないことが確認されている
Self-Attention
Query, Key, Value 全部 Source 由来とする
入力文章の各単語間の関連 = 注目している単語を特徴づける他の単語はどれか??
単語毎の特徴づけという意味では、CNNに似ている?
CNN はkernel size (一般に入力長より小さい) 内でのローカルな特徴づけ
Self-Attention は入力全体を見ることができる
例: 否定語などの、複数単語をまたぐコロケーションや、更には文脈のようなものを扱えることが期待される
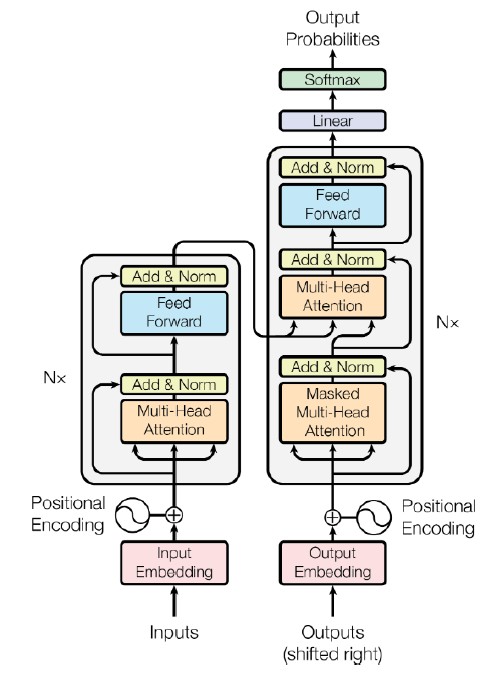
Transformer = Encoder- Decoder x Attention
RNN を使わず Attention だけで、当時のSOTAを少ない計算量で実現した
英仏3600万文字の学習を 8GPU 3.5日で終了
全体の概要は上の画像の通り。
以下では 抑えておきたいサブモジュールを簡単に解説
抑えておきたいモジュール
Multi-Head Attention (主要モジュールの②)
を, 複数セットの に対して計算
アンサンブル学習的な効果を狙って、8通りの異なる重みパラメタの注意機構を用いた。
Position-Wise Feed Forward Networks (主要モジュールの③)
Multi-Head Attention の出力のサイズを 整えるための全結合
位置(時間)情報を保持したまま順伝播させる
: 512 x 2048
: 2048 x 512,
Positional Encodgin (主要モジュール①)
Attention そのものは全結合層には時間情報を扱う仕組みを持たない
入力のEmbedding に対して 位置に対応した値を加算して位置情報を持たせる
見なくていい(未来の)単語をマスクする
PAD_TOKEN は注意する必要がない
Decoder への入力に処理中の単語より後の時刻の単語が入力されないようにマスク
Transformer の example コード解説のメモ
準備パートは seq2seq とほぼ同じ
各モジュールの定義 (直上の解説とかぶるところもあるが..)
SubLayer
Positional Encoding (これでなぜ時間情報を扱えるんや.. )
: 成分の次元
Multihead Attention
bmm は バッチ単位での内積
無視したい箇所(今回のケースではpad) で、attentionが0となるよう softmax後の値を に飛ばして
Multihead Attention 自体の実装は一つ。Q,K,V に何を与えるかに寄って、Self-Attention にも Source-Target Attention にもなる
Position-Wise Feed Forward Network
単語列の位置毎の全結合層を 1x1 conv を使って実現
1x1 conv -> relu -> 1x1 conv
Masking
key側の系列のPADトークンに対してAttention を行わないようにする
Decoder 側での Self Attention で、各時刻未来の情報へのAttention を行わない
Encoder
(Positional Encoding を用いた Embedding) + (通常のEmbedding)
Encoder Layer (Multihead Attention -> Position-wise FFN ) を 6層重ねる
モジュールList を使って for 文で回す
Decoder
(Positional Encoding を用いた Embedding) + (通常のEmbedding)
Self-Attention 用の mask
dec_input が PAD のところ、 query からみて 未来に対応するところ をマスクする
Decoder Layer x 6 層
Self-Attention (Q,K,V 全てに decoder input が入る)
Source-Target Attention (Q には decoder output , K,V には encoder output が入る)
Position-wise FFN
Encoder -> Decoder -> 線形変換
Section.6 : 物体検知・セグメンテーション
本Section のスコープ
物体検知の学習を進めたり、論文を読む上で大前提となる共通知識を取り扱う
広義の物体認識タスク (どれも入力は画像で、ラベルを出力する)
"得ようとしている情報が 大まか"な順に並べる
分類 : Classification
出力 = "画像に対して" 単一または複数のクラスラベル
画像内の対象が含まれるか否か? だけが問題
物体検知 : Object Detection
出力 = Bounding Box (bbox/BB)
矩形領域でざっくり位置も検出, インスタンスは区別しない
意味領域分割 : Semantic Segmentation
出力 = "各ピクセルに対して" 単一のクラスラベル
ピクセル単位での検出だが、インスタンスの区別はしない
個体領域分割 : Instance Segmentation
出力 = "各ピクセルに対して" 単一のクラスラベル
semantic segmentation した上で、さらに 対象が複数あるばあい個体毎の領域も分割
物体検知の基礎
どこに、何が、どの程度のconfidence (確率と厳密にイコールではないのでこう呼ぶ) で?
データセット
why dataset? -> 目的に応じて適切なデータセットを選択できるようにしたい
例えば...
クラス数
必ずしも多ければいいというわけではなく、データセットの質にも注意
cf. ImageNet はクラス数多いが批判もある
同じものに違うクラス名が振られている (laptop/notebook)
人が気づかないような米粒のようアリにまでラベルが..
Box/画像 (1画像に含まれるBoxの平均数)
目的に応じたBox/画像 (1画像あたりのBox数平均)の選択をする
大 -> 物体どうしの重なりやサイズ違いなどを扱う必要がある、実践的
小 -> 日常的に撮影される写真などとは異なるが、対象がアイコン的な写っている画像を扱う場合にはよい。
代表的データセット (どれも物体検出コンペティションで用いられたもの)
VOC12
PASCAL VOC Object Detection Challenge 2012で用いられたもの
2012年、主要貢献者がなくなり 本コンペは終了
クラス: 20, Box数/画像: 2.4
Train+Val : 11,540
画像サイズ 470x380
個々の物体にラベルが与えられている
ILSVRC17
ILSVRC(ImageNet Scale Visual Recognition Challenge) Object Detection Challenge
2017年にコンペ終了 (後継: Open Images Challenge)
ImageNet (21841 クラス/1400万枚以上)のサブセット
クラス 200, Box数/画像: 1.1
Train+Val : 476,668
画像サイズ 500x400
個々の物体にはラベルが"ない"
MS(Microsoft) COCO18
クラス : 80, Box/画像: 7.3
Train+Val : 123,287
画像サイズ 640x480
個々の物体にラベルが与えられている
OICOD18
OIC(Open Images Challenge) Object Detection Challenge
Open Images V4 (6000クラス以上/900万枚以上のサブセット)
クラス : 500, Box/画像: 7.0
Train+Val : 1,743,042
画像サイズ 一様ではない
個々の物体にラベルが与えられている
評価指標
(復習) Confusion Matrix
Positive/Negative は予測の結果、True/Falseは予測の正否
例: TN(TrueNegative) = 予測結果はnegative でありその正否は正しい (両方Negative)
Precision = TP / (TP+FP) , Positive と予測したもののうち 実際にPositive だったもの (過剰検出のすくなさ)
Recall = TP / (TP+FN), 真のラベルがPositive のもののうち、Positiveと予測したもの (取りこぼしのすくなさ)
Confidence のしきい値変化に対する振舞い
クラス分類: 1画像に対して必ず1ラベルが出力される -> confusion matrix の各マスに入る数字の合計は、しきい値を変えても 変わらない
物体検出: 1画像に対して、その閾値を超える(一般には複数の)BBが出てくる -> しきい値を変えることによって、出力されるBB数の合計が変わる -> Confusion Matrix に入る数字の合計は変わる
IoU : Intersection over Union
定義: (Area ov Overlap) / (Area of Union)
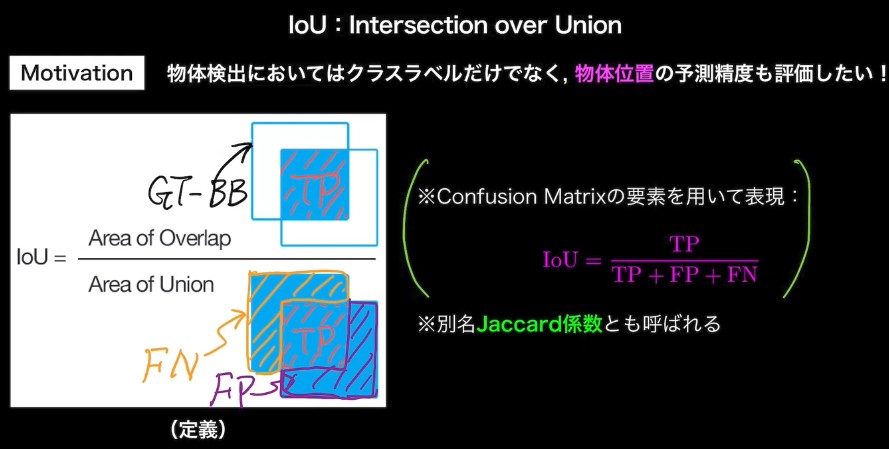
共通部分 / (Ground Truth BB) だと Predicted BB を画像全体にすれば スコアが上がってしまう
共通部分 / (Predicted BB) だとPredicted BB を小さくして、Ground Truth 内に完全に包含されれば スコアが上がってしまう
Confidence とともに、位置推定の精度の良さを表す指標としてしきい値を設定
Precition/Recall の計算方法
入力画像1枚のケース
基本的には、confidence が所定のしきい値(例 0.5)以上かつ、IoUが所定のしき値(例 0.5)以上のものを TPとする
ただし、画像に含まれる対象のBBの数 < Positive な BB数 の場合、confidence が高いものをTPとし、過剰な分は FP とする
TP, FP がきまったので、Precision そのまま計算できる
検出できなかったクラスがあれば、それを FNとして、Recall を計算 (つまり分母は 全Ground Truth の数となる)
複数画像 (クラス単位) の計算例
TP, FP の決め方は、入力画像1枚のケースと同じ
TP, FP は画像をまたいでカウントし計算
AP (Average Precision)
IoUを固定した状態で、confidence を変化させ、"クラスラベルごとに" Precision, Recall を計算
Precision を Recall の関数 で表したとして,,
: Precision-Recall curve の下側面積
実際には、confidence は離散値なので、実際には和文として計算する
mAP (mean Average Precision)
全クラスでのAPの平均値
論文などで、"AP" と書かれていても、実は mAPのこともある
「どのデータセットでの結果なのか?」も気をつける
参考
IoUを 0.5から 0.95 まで 0.05刻みで変えながら、mAPを計算して、算術平均
IoU が x の場合の mAP を とすると,,
FPS (Frame per Second)
応用上の陽性で、検出速度も評価されることがある
FPSは単位時間あたりの処理可能な枚数だが、Inference Time (1枚の画像を処理するための時間) で評価されている場合もあり
物体検知の大枠
2012年: AlexNet の登場を皮切りに 時代はSIFT特徴量をベースとした手法から、(Deep)CNNへ
2013年~
画像系の代表的なネットワーク
VGGNet, GoogleNet, ResNet, Inception-ResNet, DenseNet, MobileNet, AmoebaNet など..
物体検知のフレームワーク(抜粋)
2段階検出
候補領域の検出と、クラス推定を別々に行う
相対的には精度が高く、計算量が大きい傾向
例: RCNN, SPPNet,
1段階検出 RCNN, YOLO, SSD, ...
候補領域の検出とクラス推定を同時に行う
相対的には精度は低いが、計算量が少ない傾向
例: SSD, YOLO,..
1段階検出器の例 : SSD (Single Shot Detector)
超概要
BB を適当な位置に適当な大きさで、用意する (Default Box)
Default BOX を変形して、Predicted BB とし、conf. も出力
SSDのネットワークアーキテクチャの特徴
ベースネットワーク (VGG16) 論文
合計 16層 : Convolution 層が 13, 全結合層 3 層 (pooling 層や, ReLU単体は数えてない)
SSDの徳用
入力サイズに応じて SSD300, SSD512 など
VGG16 の FC2層がConvolution層に、最後のFCは削除
VGG16 の 10層目以降、複数の層の出力から、最終出力がつくられている (マルチスケール特徴マップ)
より解像度の高い特徴マップで小さい物体を検出している
出力
k * (クラス数 + 4) * m * n
k: Default box の数をコントロールするハイパパラメータ
+4: Default Box の中心座標の変更量 , サイズの変更量
m * n : 特徴マップのサイズ
つまり、default box 数は k * m * n
青,赤でk=4だったり、6だったりするのは演算量などの都合
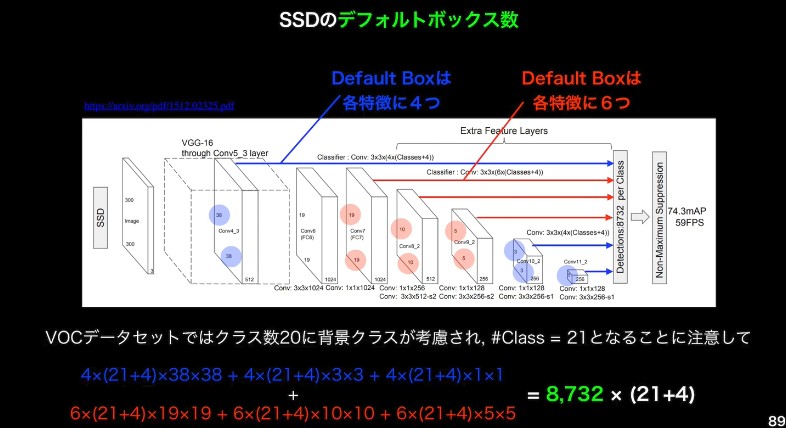
その他の工夫
1つの対象に対して、複数のBBがでてきてしまう
Non-Maximum Supression : IoU がある程度高いもののなかから、最も confidence の高いものを残して他のBBは削除する
背景(Negative)と判断されるクラスに属するBBがたくさん出てしまう
Positve : Negative の比が 偏りすぎないように 背景に属するBBを減らす
以上は、SSDの中で初出の方法では無い
Data Augmentation や、Default Box のアスペクト比のなど
損失関数
confidenct と location に関する誤差の和 (数式は割愛)
Semantic Segmentation の基礎
ざっくりわかる Semantic Segmentation の肝
convolution , pooling を繰り返すことで解像度が落ちていく
対して、出力は、"ピクセルごとの" ラベル
元の解像度に戻す Up-Sampling をいかに行うか? が Semantic Segmentation を理解するポイントになる
無邪気すぎる疑問 : そもそも Pooling しなければいいのでは?
例えば 犬/猫 判定。ごくごく一部の少領域だけでは不可能 -> 正しく認識するためには、受容野(kernel)にある程度の大きさが必要
受容野を広げるための代表的な手段
深い Conv 層
プーリング や ストライド
Dilated Convolution (後述)
Conv層の多層化は、演算量、メモリの制約もあるので、プーリング・ストライドの併用は実用的には必須
ネットワークの形
VGG16 をベースに最後 FCをConv層に置き換え (Fully Convolutional Network)
アップサンプリング方法
Deconvolution / Transposed convolution
計算例: input 3x3 -> output 5x5 ( kernel size = 3, padding = 1, stride = 1)
特徴マップのピクセル間隔を stride 分だけあける
特徴マップの周りに ( kernel size - 1 ) - padding だけ余白を作る
畳み込み演算を行う
厳密には、畳込みの逆演算ではない
輪郭情報の補完
高いレイヤーのpooling層出力は、低解像度になっていて輪郭情報が失われる -> 低レイヤーPooling層の出力を要素ごとに足すことで、輪郭情報を取り戻す
U-Net における Skip-connection では、チャネル方向にデータを結合のためやっていることは異なるが、着想, 対処したい問題は似ている
UnPooling
MaxPooling を行うとき、どこに最大値があったかを記録(Switch Variables)しておく
UnPooling では、Switch Variables の箇所に値をいれ、他をゼロで埋める
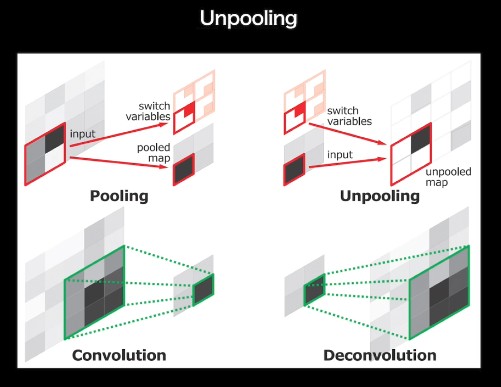
Dilated Convolution
pooling を用いずに受容野のサイズを広げる他の手段。とびとびフィルタ。
例: kernel 3x3, dilation rate=2 の場合、一つおきに畳み込むことで 5x5 の範囲をカバーすることができる
section. 7 : GAN
レポート課題にはなっていないが、ついでなのでまとめておく
GAN(ギャン) (Generative Adversarial Nets)
生成機と識別機を競わせて学習する生成 & 識別モデル
Generator : 乱数から真データと同じ形式(同じ定義域をもつ)データを生成
Discriminator : 入力データが真データ(学習データ)である確率を出力
"2プレイヤーのミニマックスゲーム" 的な学習
Generator は Discriminator に誤判断させたい
Discriminator 真偽判断の正答率を最大化したい
問題:
この価値関数は、真偽判別における、複数データに対するバイナリークロスエントロピー(に-1)かけたものと考えられる
について
真データを扱うときは を代入し、真データの分布 のもとで期待値をとる
生成データを扱うときは を代入し、生成データの分布 のもとで期待値をとる
両者をたす
最適化方法 : 以下のループを回す
Discriminator のパラメータ の更新
Generator のパラメータ を固定し、
真データ, 生成データをmコずつサンプリングして、勾配"上昇"法で 回 更新
Generator のパラメータ の更新
Discriminator のパラメータ を固定し、
生成データをmコサンプルして、勾配効果法で "1回" 更新
なぜ Generator は本物のようなデータを生成するのか?
価値関数最大の時 であると示せばよい
Step.1 : 価値関数最大の を求める
積分変数を にするため 分布 に関する書き方に変えた
と置く
が最小になるのは、
Step.2 : 価値関数が最小になる を求める
は JSダイバージェンス
の時に最小値 0 となる 分布間距離をはかる関数.
これにより、 の時 価値関数 は最小となる。
DCGAN (Deep Convolutional GAN)
GAN を利用した画像生成モデル
Generator (乱数ベクトルから画像を生成)
Pooling 層のかわりに 転置畳み込み (deconvolutionと昔よばれてた) 層を使用
活性化関数は、最終層は tanh, その他は ReLU
Discriminator (画像から真偽確率を出力)
Pooling 層の代わりに 畳み込み層を使用
活性化関数は Leaky ReLU
common
中間層に全結合層を使わない
バッチノーマライゼーションを使用
GAN を用いた応用技術
Fast Bi-layer Neural Synthesis of One-Shot Realistic Head Avatars
E. Zakharov, et al. ECCV, 2020
1枚の顔画像から、動画像を生成する問題を解ける
モチベーション
顔アバター生成の一般的な手法は、人物の特徴を抽出する初期化部 + 所望の動きをつける推論部で構成される。
(初期化部のコストは大きくてもいいので) 推論部の計算コストが小さくすることでリアルタイム推論を可能にしたい
アプローチ
初期化時にポーズに非依存な輪郭情報を取得しておき
推論時には荒い動画像と、Warping Field を生成
推論の出力 = (荒い動画像) + (Warping Field) * (輪郭情報)
コード例Link
github の studyai-team/Face_App に上がっている
動画像でなく1フレームの静止画を出力する例
取り組み概要 & 感想
取り組みの記録
今までのステージでは、レポート作成 -> ステージテストの順番でとりくんできたが、 今回は、ステージ3終了直後から、M4MT の E資格受験資格認定テストコースに参加したため、 テストから先に取り組んだ.
ざっくりの取り組み方は下記の通り。実装演習がすくないため大体、1日1セクション終わらせる感じでスムーズにすすめることができた。(メモのまとめは大体動画再生時間)
6/7 : E資格受験資格認定テストコース 1st trial (82点 -> 2点不足で不合格..) 2h
6/8 : M4MT初回 -> テスト 2nd trial -> 85点で合格 0.5h
6/11: RNN 動画メモまとめ 5h
6/12-13: RNN の逆伝播計算を自分でやる 4h
6/15: RNNの実装演習の実行 1.5h
6/18: LSTM, GRU 1.5h
6/17: 双方向RNN 1h
6/18: seq2seq 1h
6/21: word2vec, Attention 0.5h
6/22: 強化学習 1.5h
6/23: Alpha go 1h
6/24: 軽量化・高速化 1.5h
6/25: 応用モデル 1.5h
6/26: 物体検出 1.5h
6/27: GAN 1.5h
6/28: Transformer 3h
合計 28.5h 程度か。
感想ほか
講義動画・資料について。
day3と day4 強化学習~応用モデル
ステージ3と同じ先生。傾向ステージ3と同じく、雰囲気だけ理解する分にはよいのだが、説明の仕方が微妙だったり、単純に説明自体に間違い?と思われる箇所があったりしてコードを自分で書けるくらいに理解しようとすると、結構時間をくってしまった。
物体検出
わかりやすい.
時系列でどのように手法が開発されてきたか概観できたこと、データベース間の特徴の違いなどがわかってよかった.
自分が何かしらの研究分野についてまとめて、人に発表するときのお手本にしたい感じ
GAN
わかりやすい。
特に、最適性の証明や、学習のステップを追う毎に、確率分布がどのように変化していくかなどの説明が平易でわかりやすい。
最後の応用については、手法そのものの概要を説明されていたが、GANのsection で取り上げられるのであれば、具体的に応用例の中でどのようにGANが役に立っているか、使われているか、などにフォーカスした説明だとよかった。
Transformer
言語モデルの説明がとてもわかりやすい。
Transformer の 主要ブロックの説明については、今回のような定性的な説明で十分とおもうが、焦点をあてているという Attention については、Transformer のなかでの Attention の具体的な振舞いの紹介していただけるとよかった。
day3, 4 は Simple RNN 以外はまともにコードを読み書きしていないし、本当に定性的な説明を見聞きしただけなので、試験をパスする・開発での実践、どちらの対しても色々足りていない感じはする。黒本や練習問題を解きながらも、シラバスで紹介されたネットワークを自分で組んで学習させてみるなどしてみようかと考えている。
E資格受験資格認定テストについて。 E資格のテストを意識してか、これまでのステージテストとは違い Stage.4 までの資料・動画を見るだけでは解けない知識問題が数問あった。 調べればすぐにわかることだし(特に調べながら解くことは禁止されていないという認識)、仮にそれらの問題が未回答だとしても、ギリギリ合格基準は超えられるはずなので、 基本的には、ラビットチャレンジでこれまで学習してきた内容の理解をそのまま問う形だと思った。
今後の計画
ラビットチャレンジ実施の計画 & 実績がこれ.
~2021/2/15 : スタートテスト (2021/02/07完了, 10h)
~2021/3/30 : ステージ1 (2021/03/30完了, 8h)
~2021/5/6 : ステージ2 (2021/05/06完了, 21h)
~2021/5/30 : ステージ3 (2021/06/02完了, 17.75h)
~2021/6/27 : ステージ4 (2021/07/05完了, 26h)
~2021/7/4 : 復習 -> 修了テスト (2021/06/08完了,2.5h)
今後の計画は少しだけ復習.
~2021/7/20 : EもぎLite, 黒本
~2021/7/30 : シラバスにある未学習箇所の学習
~2021/8/26 : 今までの復習
2021/8/27,28: E資格 受験
ラビットチャレンジ関連次回の投稿は、試験直前期のレポート & 合格報告となる予定です!