ラビットチャレンジ: Stage.3 深層学習 Day1, 2

本ページはラビットチャレンジの、 Stage.3 "深層学習 Day1,2" のレポート提出を兼ねた受講記録です。 提出指示を満たすように、下記の方針でまとめました。(事務局にも問い合わせて問題ないことを確認した)

1. 動画講義の要点まとめ

   • 自分が講義の流れを思い出せるようなメモを残す。通常であれば要点として記載すべき図・数式などがあっても、それが自分にとって既知であれば、言葉の説明ですませることもある

2. 実装演習

   • 各Sectionで取り上げられた .ipynb or .py ファイルの内容を実行した結果を記載

   • ただし、初学者向けにやや冗長な内容がある場合、抜粋することもある

3. 確認テスト

   • 確認テストの解答に相当する内容は、個別の節をもうけず、要点まとめに含めたり、コードに対するコメントとして記載する

     • 確認テストは重要事項だから、出題されているのであって、まとめ/演習と内容がかぶるはず。

     • 事務局がレポートチェックをする時のために、(確認テスト:1-2) のようなタグを付す。１つ目の数字が section番号、２つ目の数字が 「何番目のテストか?」

4. 1~3 をまとめる上で思うことがあれば、考察やコメントも適宜残しておく。

目次

Day1

プロローグ　

• 機械学習/DLモデルが解こうとしている問題

  • 識別 (discriminateve, backward)

    • データ $\bm{x}$ -> クラス $C_k$

      • $p (C_k | \bm{x})$ を計算する (確率最大となる $C_k$ を分類結果にする)

      • 例: 画像認識 ( 犬やネコの画像データを入力すると、犬なのか、ネコなのかを出力する)

    • 高次元 -> 低次元

      • 学習データは比較的少なめ

    • モデルの例

      • 決定木, ロジスティック回帰, SVM, NN

    • 開発のアプローチ (Phase.2でやった話)

      • 生成的アプローチ

        • $p(\bm{x} | C_k) , p(C_k)$ をモデル化・推定し、 ベイズの定理から $p(C_k| \bm{x})$ を計算する

          • データの分布 $p(\bm{x}|C_k)$ は分類結果よりも複雑なことがある。

            • その分学習コスト大。

            • 単純に分類結果を得たいだけならば、識別的なアプローチを用いる。

            • 副産物として得られた生成モデルを活用したい場合は良い。

        • 確率的な識別ができる。(識別的アプローチと同様)

• 識別的アプローチ

  • 直接 $p(C_k| \bm{x})$ をモデル化・推定する

  • 確率的な識別

    • 機械学習のモデルの出力は 事後確率 $p(C_k|\bm{x})$ であり、そこからどのように識別結果を得るかは、開発者の裁量。

    • 自信のある無しの度合いを測ることができる。

  • 学習コスト中

  • 確率的識別モデル

• 識別関数

  • 入力 $\bm{x}$ から 出力のクラスへの写像 $f(\bm{x})$ を直接推定

  • 学習データ・コストが少ない。決定的な識別

  • 決定的識別モデル

• 生成 (generative, forward)

  • クラス $C_k$ -> データ $\bm{x}$

    • $p (\bm{x}|C_k )$ の分布情報を持った上で、サンプリングする。

      • データの分布は複雑になりがち。実際に

    • 例: 犬の画像くれ、といったら 犬の画像っぽいものを出力してくれる, テキスト生成、画像の超解像など

  • 低次元 → 高次元

    • 学習データは大量に必要

  • モデルの例

    • HMM, ベイジアンネットワーク, VAE, GAN

• 万能近似定理

  • 非線形の活性化関数を持つNeuralNetworkは任意の関数を近似できる

1. ニューラルネットワークの全体像

• 入力層、中間層、出力層で構成される

  • 識別モデルの例では、入力層のノードにあたるのはデータ、出力層のノードはそれぞれのクラスに属する確率。

  • (確認テスト:0-1)

    • ディープラーニングがやろとしていること

      • 入力されたデータを変換して所望の出力に変換する数学モデルをつくる

      • ここで使用されるのはパラメータを持つ中間層を複数使用して高い自由度が得られるようなモデル

    • 学習によって最適化するのは

      • パラメータ　(3. 重み と 4. バイアス)

• 数式も用いて説明

  • (確認テスト:0-2) 入力層2ノード, 中間層3ノード 出力層1ノード のネットワーク

• ニューラルネットワークでできること

  • 回帰 : (主に) 連続的な実数値を取る関数の近似

    • 例

      • 結果の予想 (売上、株価など)

      • ランキング (競馬順位, 人気順位)

    • NN以外の手法

      • 線形回帰, ランダムフォレスト、回帰木

  • 分類 : 数値の大小関係に意味のない、離散的な結果を予想するための分析

    • 例

      • ネコ写真判別

      • 手書き文字認識

      • 花の種類分類

    • NN以外の手法

      • ベイズ分類, ロジスティック回帰, 決定木, ランダムフォレスト

• 深層学習の実用例

  • 深層学習モデルはとても表現力が高いため、入力と出力を数値・ベクトルに変換してしまいさえすれば、あらゆる問題に応用できる可能性がある

  • 例えば、自動売買、チャットボット、翻訳、音声解釈、囲碁/将棋AI など

1. 入力層-中間層

• (確認テスト:1-1) 入力層~中間層の図に Section.0で取り上げた動物分類の実例を書き入れてみると以下のようになる

  • 

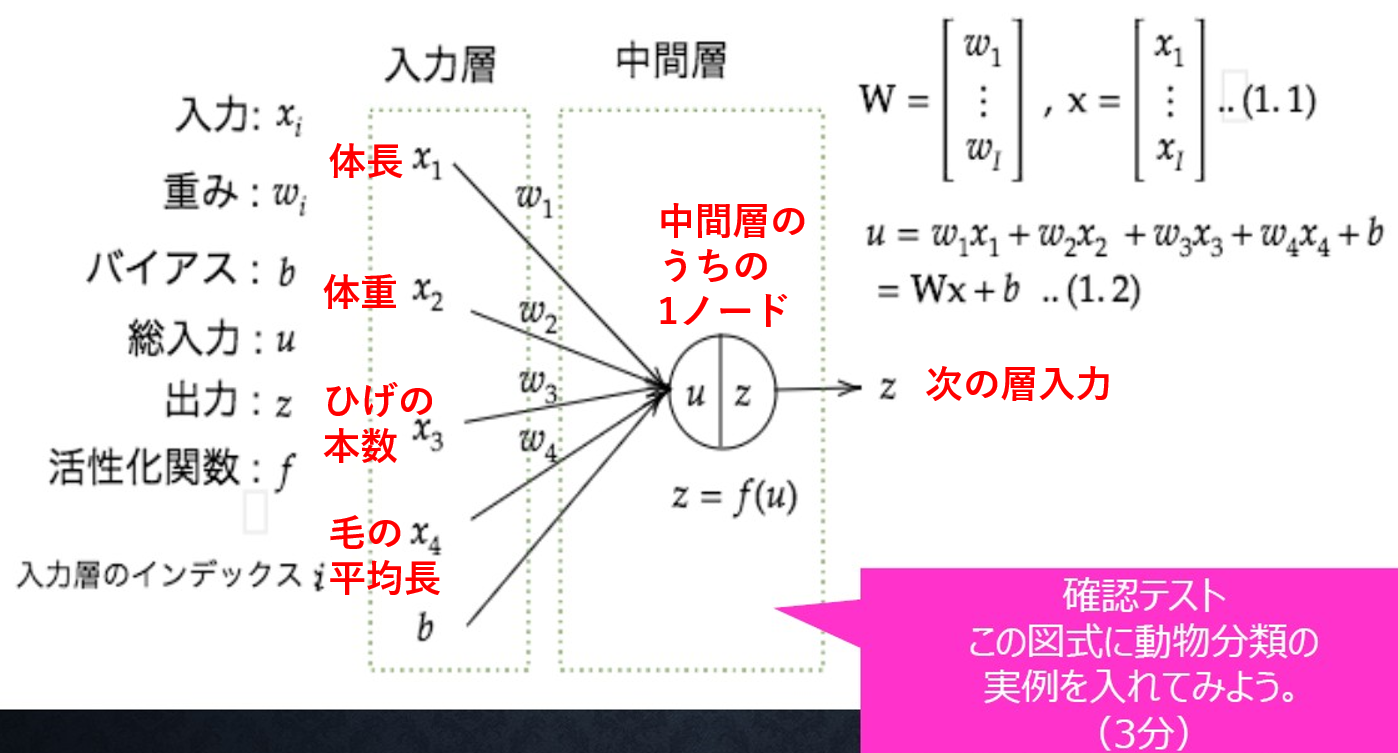
  • 愚痴コメント: "この図式に"実例を入れると書いてあるのだから、入力4次元のNNに合わせて実例の方を変えるべきですよね.. (模範解答のような回答を期待しているのならば、「実例の図から、この図式のような形で入力層~中間層までに相当する部分を抜き出せ」というような問題文になるはず)

• $u=\sum_{i=1}^4 w_i x_i + b$ の変換を行い、それが次の中間層の入力となり、活性化関数がかかって中間層の出力となる

  • 学習に置いては、この $w_i, b$ が最適化される

  • 各計算式に対応する箇所は、実装演習のコードにコメントした。

• "12_入力層の設計" の動画の内容

  • 深層学習モデルに入力するには、とにかく対象を数値ベクトルにすればよい

    • 例: カテゴリ変数のようなものも フラグ値として定義可能

      • 犬・ネコ・ネズミの三種のいずれかを表したい場合、犬=[1,0,0], ネコ=[0,1,0], ネズミ=[0,0,1] などとする (ワンホットラベル,ワンホットベクトル)

  • 入力層に入れるデータの選定

    • 欠損値が多いデータ、誤差の大きいデータは学習データからは取り除く

    • 解きたい問題の"生の入力" を入れて問題が解けるのが理想

      • end2end のモデルを作るほうが全体最適なモデルができあがるはずで(理屈上は)ベター.

    • 意味なく振られた数値は使えない

      • 背番号などは必ずしも人と一対一対応しない

      • 誤差計算をするのに適切でない場合 (Yes:1 No:0, どちらでもない:-1, 無回答:-1)

        • 別の意味を持つ回答が同じ数値に割り当てられている

        • Yes - No = 1, No - 無回答= 1 両者の違いが等しいわけではない

        • -> これらの問題を解決するには、ワンホットベクトルを使う

  • 入力データの加工例

    • 欠損値の扱い

      • ゼロで埋める

      • 欠損値がやたらと多い説明変数はそもそも使わない

      • 色々な次元で欠損値があるサンプルはそもそも使わない

    • 数値の正規化・正則化

      • 正規化: (絶対値の)最大値で割って -1 ~ 1 とか、0~1 の範囲におさめる

      • 正則化: 平均0, 分散を1にする

    • データの結合

      • 読んで時の通り。中には、数量的なデータとカテゴリ変数だったものを(ワンホットエンコードして)結合するようなこともある

実装演習抜粋 ( 順伝播（3層・複数ユニット）)

数式では、$Wx+b$ なのに python では np.dot(x,W) となる? np.dot() 関数の挙動をしっかり抑えておく必要がある。

• 基本の動作は行列積(のようなもの)

  • 要素数が一致する次元: a の最後の axis と b の 最後から2番目のaxis

  • 通常の行列積も包含

• 下記が適応不可能な自体では、よしなにそれっぽい計算が行われる

  • 例:

    • if a,bの両方orどちらかがスカラー: 普通の積. (スカラーをもう一方の全要素にかける)

    • elif b がベクトル: a の最後の axis と b の長さが一致

      • ベクトルの内積のケースも包含

# 順伝播（3層・複数ユニット）

# ウェイトとバイアスを設定
# ネートワークを作成
def init_network():
    print("##### ネットワークの初期化 #####")
    network = {}
    
    # 試してみよう
    #_ネットワークの初期値ランダム生成
    network['W1'] = np.random.rand(2,3)
    network['W2'] = np.random.rand(3,2)
    network['W3'] = np.random.rand(2,2)
    network['b1'] = np.random.rand(3)
    network['b2'] = np.random.rand(2)
    network['b3'] = np.random.rand(2)

    # 試してみよう
    #_各パラメータのshapeを表示
    print("*各パラメータのサイズ情報")
    for k,v in network.items():
        print("network[%s].shape=" % k, end='')
        print(v.shape)
    print()

    # 変更前
    # network['W1'] = np.array([
    #     [0.1, 0.3, 0.5],
    #     [0.2, 0.4, 0.6]
    # ])
    # network['W2'] = np.array([
    #     [0.1, 0.4],
    #     [0.2, 0.5],
    #     [0.3, 0.6]
    # ])
    # network['W3'] = np.array([
    #     [0.1, 0.3],
    #     [0.2, 0.4]
    # ])
    # network['b1'] = np.array([0.1, 0.2, 0.3])
    # network['b2'] = np.array([0.1, 0.2])
    # network['b3'] = np.array([1, 2])

    print_vec("重み1", network['W1'] )
    print_vec("重み2", network['W2'] )
    print_vec("重み3", network['W3'] )
    print_vec("バイアス1", network['b1'] )
    print_vec("バイアス2", network['b2'] )
    print_vec("バイアス3", network['b3'] )

    

    return network

# プロセスを作成
# x：入力値
def forward(network, x):
    
    print("##### 順伝播開始 #####")

    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    # 1層の総入力
    u1 = np.dot(x, W1) + b1  # (確認テスト:1-2) 入力層の計算に該当
    
    # 1層の総出力
    z1 = functions.relu(u1)  
    
    # 2層の総入力
    u2 = np.dot(z1, W2) + b2
    
    # 2層の総出力
    z2 = functions.relu(u2) # (確認テスト:1-3) 中間層の出力に該当

    # 出力層の総入力
    u3 = np.dot(z2, W3) + b3
    
    # 出力層の総出力
    y = u3
    
    print_vec("総入力1", u1)
    print_vec("中間層出力1", z1)
    print_vec("総入力2", u2)
    print_vec("出力1", z1)
    print("出力合計: " + str(np.sum(z1)))

    return y, z1, z2

# 入力値
x = np.array([1., 2.])
print_vec("入力", x)

# ネットワークの初期化
network =  init_network()

y, z1, z2 = forward(network, x)

*** 入力 ***
    [1. 2.]
    
    ##### ネットワークの初期化 #####
    *各パラメータのサイズ情報
    network[W1].shape=(2, 3)
    network[W2].shape=(3, 2)
    network[W3].shape=(2, 2)
    network[b1].shape=(3,)
    network[b2].shape=(2,)
    network[b3].shape=(2,)
    
    *** 重み1 ***
    [[0.46325703 0.4515028  0.9015613 ]
     [0.63300315 0.09960203 0.35035177]]
    
    *** 重み2 ***
    [[0.85561969 0.64270626]
     [0.71017196 0.35407221]
     [0.21520079 0.12526929]]
    
    *** 重み3 ***
    [[0.04970514 0.3372038 ]
     [0.80197002 0.34030274]]
    
    *** バイアス1 ***
    [0.14282813 0.02490021 0.42369957]
    
    *** バイアス2 ***
    [0.16724682 0.77646073]
    
    *** バイアス3 ***
    [0.97460445 0.08008213]
    
    ##### 順伝播開始 #####
    *** 総入力1 ***
    [1.87209147 0.67560708 2.02596442]
    
    *** 中間層出力1 ***
    [1.87209147 0.67560708 2.02596442]
    
    *** 総入力2 ***
    [2.6848315  2.47267045]
    
    *** 出力1 ***
    [1.87209147 0.67560708 2.02596442]
    
    出力合計: 4.573662972619907

2. 活性化関数

• 活性化関数

  • 次の層への出力を決める (一般的には)非線形の関数

    • Section.0 の図中の関数 $\mathbf{f}$ に相当

  • (確認テスト:2-1) 線形と非線形

    • 図にすると

      • 線形

      • 非線形

    • 線形な関数は、加法性 $f(a+b) = f(a) + f(b)$ と 斉次性(作用素との可換性) $f(ab) = a f(b)$ を満たす

    • 非線形な関数は、その名の通り、線形な関数 "以外"

  • 活性化関数の例

    • 中間層で用いられる代表例

      • ステップ関数

        • パーセプトロンで使われていた経緯があるが 0 or 1 しか表せないので 線形分離可能なものしか識別できないということで最近は使われない

      • シグモイド関数

        • すべての点で微分可能で扱いやすいが、勾配消失問題を引き起こしやすい

      • ReLU関数

        • シグモイドに比べれば勾配消失問題を起こしにくい

        • スパース化に貢献

    • 出力層でもちいられる代表例

      • ソフトマックス関数

      • 恒等写像 (これは非線形関数じゃないから)

実装演習抜粋 (順伝播 単層・複数ユニット）

# 順伝播（単層・複数ユニット）

# 重み
W = np.array([
    [0.1, 0.2, 0.3], 
    [0.2, 0.3, 0.4], 
    [0.3, 0.4, 0.5],
    [0.4, 0.5, 0.6]
])

## 試してみよう_配列の初期化
#W = np.zeros((4,3))
#W = np.ones((4,3))
#W = np.random.rand(4,3)
W = np.random.randint(5, size=(4,3)) # randint を試してみた例

print_vec("重み", W)

# バイアス
b = np.array([0.1, 0.2, 0.3])
print_vec("バイアス", b)

# 入力値
x = np.array([1.0, 5.0, 2.0, -1.0])
print_vec("入力", x)


#  総入力
u = np.dot(x, W) + b
print_vec("総入力", u)

# 中間層出力
z = functions.sigmoid(u)  # (確認テスト:2-2) 
print_vec("中間層出力", z)

*** 重み ***
    [[3 1 4]
     [3 1 0]
     [4 2 3]
     [0 3 4]]
    
    *** バイアス ***
    [0.1 0.2 0.3]
    
    *** 入力 ***
    [ 1.  5.  2. -1.]
    
    *** 総入力 ***
    [26.1  7.2  6.3]
    
    *** 中間層出力 ***
    [1.         0.99925397 0.99816706]

3. 出力層

• 誤差関数

  • その時々のパラメータを用いて、入力データから計算したモデルの出力が、どれくらい間違っているかを計算するもの

    • 予め 入力データ(NNモデルの入力)　と 訓練データ(入力データに対応する正解値)を用意しておく

  • 例: 二乗誤差和 $\frac{1}{2} \sum_{j=1}^{J} (y_j-d_j)^2$

    • (確認テスト:3-1)

      • 差を二乗する理由: 各要素毎の誤差を非負値にすることで、完全にベクトルが一致するとき以外誤差が0にならないようにするための一方法

      • 1/2 している理由: 最適化計算のための微分計算をすることになるのだが、二乗を微分してでてくる 2 と打ち消し合って式がよりシンプルになることを狙っている。

    • 通常分類問題では誤差関数にクロスエントロピー誤差を用いることが多いが、本講義では説明の便宜上平均二乗誤差が用いられる箇所がある

• 出力層の活性化関数

  • 中間層とは役割が異なるため、利用される活性化関数も異なる

  • モデル出力を解いている問題にあった使いやすい形に変換するために用いる

    • 分類問題では、入力データがどの分類クラスのデータであるかを表す確率を出力させる

      • 出力ベクトルの各要素は 0~1の範囲で、全要素の和が1

  • 例

    • 回帰問題

      • 活性化関数 : 恒等写像

      • 誤差関数 : (平均)二乗誤差

    • 二値分類

      • 活性化関数 : シグモイド関数

      • 誤差関数: 交差エントロピー

    • 多クラス分類

      • 活性化関数 : ソフトマックス関数

      • 誤差関数: 交差エントロピー

実装演習 (誤差関数定義)

厳密には、実装演習は無し。確認テストのために関数定義を確認しただけ

# ソフトマックス関数　(確認テスト:3-2)
def softmax(x):
    if x.ndim == 2: # 複数データが入力された場合のための場合分け
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x) # オーバーフロー対策 (プログラム動作を安定化させるためのもの)
    return np.exp(x) / np.sum(np.exp(x)) # この一行がソフトマックス関数の本質的な実装
    # (1) はあえていうなら return
    # (2) は分子の np.exp(x) 
    # (3) は分母 の np.sum(np.exp(x))

# クロスエントロピー (確認テスト:3-3)
def cross_entropy_error(d, y):
    if y.ndim == 1: # 次元を一つ増やして、この後の処理と整合性をとる
        d = d.reshape(1, d.size)
        y = y.reshape(1, y.size)
        
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if d.size == y.size:
        d = d.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
    # (1) はあえていうなら return
    # (2) は -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) が本質的な部分
    #    y[np.arange(batch_size), d] は 少しトリッキーだが、
    #    この関数上で yは確率ベクトルであるが、dはワンホットエンコードされたものではなく、正解ラベルである前提で
    #    np.sum() は複数データに関する足し算であって、数式上の 和とはことなる
    # + 1e-7 は logの真数を確実に正の値とするための epsilon

4. 勾配降下法

• 勾配降下法の考え方

  • 深層学習モデルを構築するための最適化手法として用いる

    • 学習 = 誤差関数 $E(\mathbf{w})$ を最小化するパラメータ $\mathbf{w}$ を見つける

    • 最適化手法には 通常 "勾配降下法" が用いられる

  • パラメータ更新式のイメージと学習率

    • (確認テスト:4-1) -> Section.5 勾配降下法の実装演習コード上にコメント付記

    • その時々のパラメータにおける勾配と逆方向にパラメータを更新する = 極小値に向かう変更

    • 学習率 $\epsilon$ はその歩幅を決める

      • 学習率が大きすぎると、最適解(=大域的極小値)を飛び越えて最悪発散する可能性がある

      • 学習率が小さすぎると、最適解にたどり着くまでの更新回数が増える(時間がかかる)

        • 小さすぎると局所解につかまるが、適切な量に設定すると飛び越えられるという説明の図(下図)は、不適切(もしくは言葉足らず)なように思う

          • 

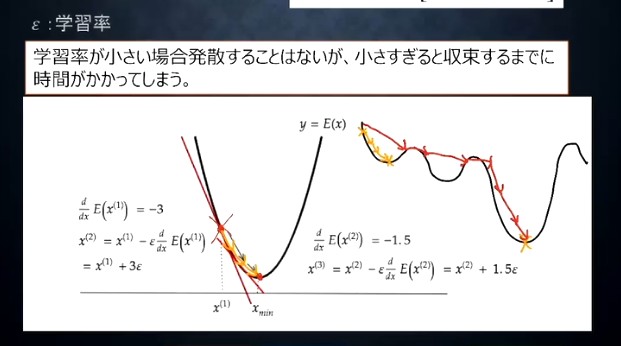
          • 説明では強引に最適解まで更新し続けるような矢印が書かれているが、、一回目の更新後の勾配は正値のためパラメータは局所解の方向に向かう。勾配の絶対値も小さいのでちょうど局所最適にハマるような絵になっている。

    • 勾配降下法ベースのパラメータ更新アルゴリズム (詳細はDay2)

      • Momentum, AdaGrad, Adadelta, Adam など。

      • Adam がよく使われる

• (バッチ)勾配降下法

  • 与えられたデータ(全部)に対する出力からエラーを計算する

  • そこから得られた勾配を使って、パラメータ(重み $W$ と バイアス $b$)を更新

  • 更新されたパラメータを用いて、次の週(エポック)へ

• 確率的勾配降下法 (SGD)

  • パラメータを更新する毎にランダムに抽出したサンプルの誤差を計算

    • 1サンプルで1回パラメータ更新

  • メリット

    • データが冗長な場合計算コストを軽減できる

    • パラメータ更新方向にランダム性をもたせることで、望まない局所解に収束するリスクを軽減する

    • オンライン学習ができる

      • (確認テスト:4-2) オンライン学習とは

        • 新しい学習データが入ってくるたびに都度パラメータを更新する学習方法。バッチ学習は一度にすべての学習データを使ってパラメータ更新を行う。

          • 大規模な機械学習・深層学習では計算機のRAM制約でバッチ学習を実施することが非現実になることがある

• ミニバッチ勾配降下法 (深層学習の場合は基本的にこのアプローチをとる)

  • ランダムに分割したデータの集合(ミニバッチ) $D_t$ に属するサンプルの誤差を使って勾配を計算する方法

    • 例: 全データ10万 = 500データ x 2000 バッチ

    • (要確認): 結局、1エポックに1回更新するのか、1ミニバッチ毎に1回更新するのか?

  • メリット

    • 確率的勾配降下法のメリットを維持しつつ、計算機の計算資源を有効利用できる

      • CPUを利用したスレッド並列化や、GPUを利用したSIMD並列化など

      • (要確認): 講師の説明では、複数のバッチを同時並行的に計算すると言っているが、私の理解では、バッチ内の複数データを並列計算するというのが、通常のミニバッチ勾配降下法の実装のされ方だと思っていた

        • 分散学習などするときには、各分散ノードで異なるミニバッチの処理を同時に行うことがあるのは知っているが、現時点でその話を想定して話をしていると考えるは無理がある..

    • (確認テスト:4-3) $w^{(t+1)}=w^{(t)}-\epsilon \nabla E_t$ のイメージ図

      • 

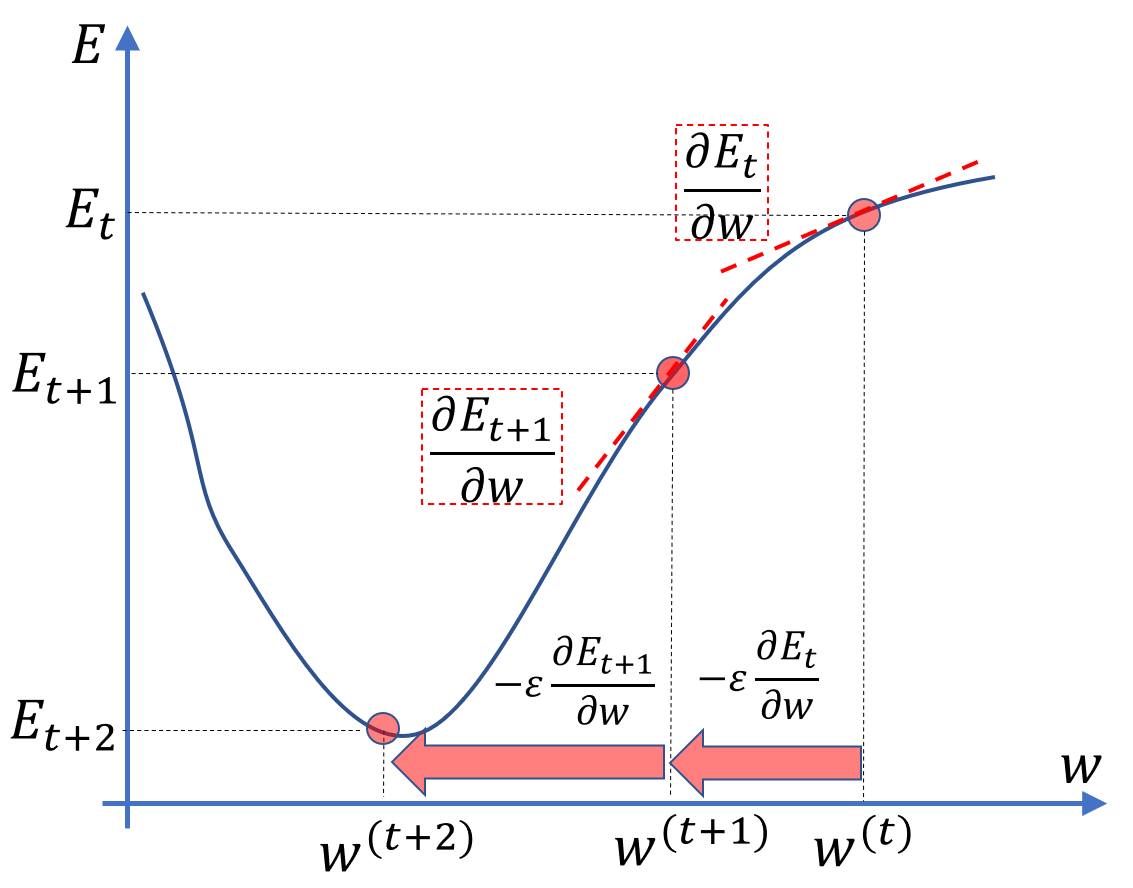
      • ミニバッチ勾配降下法の動画の中で取り上げられた文脈なので、$t$ は ミニバッチのインデックスかと思っていたが、動画では エポックのインデックスだという。。理解が間違っているのか? その辺りはぼかした図にしておく.

実装演習 (更新式定義)

厳密には、実装演習は無し? -> 誤差逆伝播法の実装演習と兼ねる。

5. 誤差逆伝播法

• 誤差逆伝播法をなぜ使うか?

  • 勾配降下法を行うためには、各々のパラメータに関する誤差関数の微分値を求める必要がある

  • 数値微分では、演算負荷が大きい。

    • $\frac{\partial E}{\partial w_m} \simeq \frac{E(w_m+h) - E(w_m-h)}{2h}$

    • 各パラメータに対して、現在の値を中心に $\pm h$ ずらした誤差関数を計算する必要があり、大量パラメータの反復更新を膨大な回数行う深層学習では、効率が悪い

  • 誤差逆伝播法は、上記と比較して効率がよい

• 誤差逆伝播法の方法

  • 合成関数の微分(連鎖律)を用いて、出力層側から順番に微分値を計算していく

    • コメント: 図を使った講師の表現が気になる..

      • 講師の表現 : "yはuになって, u は w になって"

      • 自分的にしっくりくる表現: "yはuの関数で、uはwの関数で" -> 後に講師もこの表現で説明してた.安心。

    • 例: 3層のNNの中間層の重み $\bm{w}^{(2)}$ の 1要素 $w^{(2)}_{ji}$ に関する勾配を求めるための計算

      • 連鎖律: $\frac{\partial E}{\partial w^{(2)}_{ji}} = \frac{\partial E}{\partial \bm{y}} \frac{\partial \bm{y}}{\partial \bm{u}^{(2)}} \frac{\partial \bm{u}^{(2)}}{\partial w^{(2)}_{ji}}$

      • $\frac{\partial E}{\partial y} = \bm{y}-\bm{d}$

      • $\frac{\partial \bm{y}}{\partial \bm{u}^{(2)}} = 1$

      • $\frac{\partial u^{(2)}}{\partial w^{(2)}_{ji}} = [0,\ldots,z_i,\ldots,0]^T$

  • (確認テスト:5-1) -> 実装演習コードにコメント

  • (確認テスト:5-2) -> 実装演習コードにコメント (動画で説明された模範解答は間違っていると思う..)

実装演習 (確率的勾配法のコードを用いて誤差逆伝播法を理解)

ちなみに、ファイルをダウンロードした状態では、 forward/backward で活性化関数の不一致があったため、reluに統一した (sigmoidでも同様に収束していそうなことは確認)

import sys
sys.path.append('.')

import numpy as np
from common import functions
import matplotlib.pyplot as plt

def print_vec(text, vec):
    print("*** " + text + " ***")
    print(vec)
    #print("shape: " + str(x.shape))
    print("")

確率勾配降下法

# サンプルとする関数
#yの値を予想するAI

def f(x):
    y = 3 * x[0] + 2 * x[1]
    return y

# 初期設定
def init_network():
    # print("##### ネットワークの初期化 #####")
    network = {}
    nodesNum = 10
    network['W1'] = np.random.randn(2, nodesNum)
    network['W2'] = np.random.randn(nodesNum)
    network['b1'] = np.random.randn(nodesNum)
    network['b2'] = np.random.randn()

    # print_vec("重み1", network['W1'])
    # print_vec("重み2", network['W2'])
    # print_vec("バイアス1", network['b1'])
    # print_vec("バイアス2", network['b2'])

    return network

# 順伝播
def forward(network, x):
    # print("##### 順伝播開始 #####")
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    u1 = np.dot(x, W1) + b1
    z1 = functions.relu(u1)    
    #z1 = functions.sigmoid(u1)
    
    u2 = np.dot(z1, W2) + b2
    y = u2

    return z1, y

# 誤差逆伝播
def backward(x, d, z1, y):
    # print("\n##### 誤差逆伝播開始 #####")    

    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    # (確認テスト:5-1) 微分値再利用 & (確認テスト:5-2) 各微分値の計算 -------------ここから
    # 出力層でのデルタ
    #  dE/dy = dE/dy ・ dy/du2  の計算に該当. (yとu2が恒等写像なので) 
    #  これを保存して 後に再利用していることで演算効率をあげている
    delta2 = functions.d_mean_squared_error(d, y)

    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0) # delta2 の再利用 
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2) # delta 2 の再利用, dE/dw2 = dE/dy ・ dy/du2 ・ du2/dw2

    # 中間層でのデルタ
    # dE/du1 = dE/dy・dy/du2・ du2/dz ・dz/du1 の保存
    # これを保存して 後に再利用していることで演算効率をあげている
    delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)   
    #delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1) 

    delta1 = delta1[np.newaxis, :]
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0) # delta1 の再利用
    x = x[np.newaxis, :]
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1) # delta1 の最入用
    # # (確認テスト:5-1) 微分値再利用 & (確認テスト:5-2) 各微分値の計算　該当箇所 ----- ここまで

    return grad

# サンプルデータを作成
data_sets_size = 100000
data_sets = [0 for i in range(data_sets_size)]

for i in range(data_sets_size):
    data_sets[i] = {}
    # ランダムな値を設定
    data_sets[i]['x'] = np.random.rand(2)
    
    ## 試してみよう_入力値の設定
    # data_sets[i]['x'] = np.random.rand(2) * 10 -5 # -5〜5のランダム数値
    
    # 目標出力を設定
    data_sets[i]['d'] = f(data_sets[i]['x'])
    
losses = []
# 学習率
learning_rate = 0.07

# 抽出数
epoch = 1000

# パラメータの初期化
network = init_network()
# データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)

# 勾配降下の繰り返し
for dataset in random_datasets:
    x, d = dataset['x'], dataset['d']
    z1, y = forward(network, x)
    grad = backward(x, d, z1, y)
    # パラメータに勾配適用
    # (確認テスト:4-1) 勾配降下法の更新式に対応するコード ここから
    for key in ('W1', 'W2', 'b1', 'b2'):
        network[key]  -= learning_rate * grad[key] 
    # (確認テスト:4-1) 勾配降下法の更新式に対応するコード ここまで

    # 誤差
    loss = functions.mean_squared_error(d, y)
    losses.append(loss)

print("##### 結果表示 #####")    
lists = range(epoch)

plt.plot(lists, losses) # 散布図より直線のほうが見やすいので変更
plt.show()

##### 結果表示 #####

Tips：ディープラーニングの開発環境

「その前に開発環境を紹介しておきたいとおもいます」 という一言から録画が始まってるのだが、「その前に」って何の前だろう..

• ローカルPC と クラウド環境

  • ローカルPC = 家や会社に置いてあるPC

  • クラウド = データセンター(に置いてあるPC)を間借り

    • 例: AWS, GCP

• プロセッサ

  • 各種プロセッサ (一般的には下に行くほど早いが、用意するのにお金いる)

    • CPU : 汎用演算, 高クロックだが昨今頭打ち(数GHz), 並列度低め(数十コアくらいまで)

    • GPU : ゲーム(グラフィック)特化の演算がDLに流用可能、クロックはCPUよりは低いが、並列度が高い分演算が早い

    • FPGA : 論理回路をプログラム可能 (自分で適切な演算器を設計できる) なため、高速な演算ユニットをつくることが可能

    • ASIC : Google の TPUなどが具体例。完全ハードウェアロジック化したもので、FPGAよりさらに早い

Tips: その他の一般的な機械学習の手法について

• データ拡張(Data Augmentation)

  • データ拡張の適用先

    • 分類タスクに有効

      • 様々なバリエーションに対応する必要がある

      • 新しいデータを作ることが容易(例:回転させても同じ分類をしてほしいなど)

    • それ以外のタスクには向かないこともある

      • データの密度分布を推定する問題には使えない

        • 真の分布を知らずに、真の分布の推定の助けになるデータをでっち上げるのは不可能

  • データ拡張の方法

    • 入力データ改変: 問題の性質を考慮して行う

      • オフセット, 回転など

    • モデル内部での対応: 一般的に適用可能な方法を用いる

      • ドロップアウト

      • 入力層・中間層へのノイズ注入 (バリエーションの増加)

  • 効果

    • 劇的に汎化性能が向上することがある

    • ランダム性のあるデータ拡張を行うときは再現性に注意

• 転移学習

  • 学習済みモデルをベースに、タスク固有の処理に対応する"一部の層のみ"を再学習する手法

    • cf: ファインチューニング: 全パラメータを再学習する点が違う

    • 深層学習モデルでは 前半部が汎用的な特徴抽出部、後半部がタスク固有処理部である、というような理解に基づく

Day 2 レポート

• 前半: 中間層をある程度増やした大きいネットワークを学習するときによく起こる問題

• 後半: 畳み込みニューラルネットワーク

1. 勾配消失問題

• 誤差逆伝播法の復習

  • 割愛.

  • (確認テスト:1-1) 連鎖律を使ってdz/dx を求めよ。ただし $z = t^2, t = x+y$

    • $\frac{d z}{dx} = \frac{d z}{dt} \frac{dt}{dx} = 2t \dot 1 = 2(x+y)$

• 勾配消失問題

  • 誤差逆伝播法で出力から入力に向かって計算をすすめていくにつれて勾配がどんどん緩やかになっていくことで、入力層に近い側の層のパラメータがほとんど変わらず、最適値に収束しなくなる

    • 微分値は 大きさ0~1の間をとるものが多い

      • (確認テスト:1-2) sigmoid 関数の 傾きは 0~0.25 (答えは (2) 0.25 )

        • sigmoid 関数 $\sigma$ の微分 $= (1-\sigma) \sigma$

      • 中間層で sigmoid を使うと、1層遡るたびに 0.25よりも小さい値が掛け算されていく

• 勾配消失問題の対策方法

  1. 活性化関数の選択

  • 勾配消失が起きづらい(微分値が小さくならない) 活性化関数を使う

  • 例: ReLU関数 $f(x) = \mathrm{max}(0,x)$

  • 0 より大きいときは、微分値1 -> 勾配消失問題を回避

  • 0 より小さいときは、微分値0にする -> このノードを経由しての誤差は伝播しない -> スパース化

  2. 重みの初期化方法の工夫

  • 重みは適切に設定する必要がある

    • (確認テスト:1-3) たとえばすべての重みを0に設定すると、正しい学習が行えない

      • すべての重みの値が均一に更新され、多数の重みを有効に働くモデルが学習できない。(モデルが持つ自由度を発揮でない)

  • Xavier (ザビエル) の初期値設定法

    • sigmoid 等 S字カーブ系の活性化関数を使う時に有効

    • 標準正規分布(平均が0, 分散が1 )に従った乱数 を 前のレイヤーのノード数のルートで割る

      • 補足資料: 5つの中間層を持つNN の各層の出力のヒストグラムの観察

        • 標準正規分布で初期化した場合

          • 各層の出力のヒストグラムを見ると、0付近 と1付近に集中する -> sigmoid 使った場合勾配が非常に小さくなるので、勾配消失問題が起きやすい状態

        • 標準正規分布を小さな値で割った値(標準偏差を小さくする)で初期化した場合

          • 各中間層の出力は 0.5 付近に集中する -> 何を入れても出力が似通っている -> モデルが仕事してない状態

        • Xavier の初期化を使用した場合

          • 各層の出力は、適度に0から1の間でバラツキがあっていい感じの出力が得られていそう

  • Heの方法

    • ReLU 関数に対して使う

    • 正規分布を $\sqrt{\frac{2}{N}}$

      • 補足資料: 各層の出力

        • 標準偏差が1のとき -> ほとんど出力が0による

        • 標準偏差をもっと小さくした時 -> やはり出力が0による

        • He の初期化 -> いい感じ

  3. バッチ正規化 (batch normalization)

     • ミニバッチの単位で入力データの偏りを抑制する

       • バッチ内データを平均0分散1に正規化する($\hat{x}$とする)

       • $y=\gamma \hat{x} + \beta$ ($\gamma, \beta$ スケール・シフトの微調整を行うパラメータとして学習される)

     • (確認テスト:1-4) 期待される効用

       • 収束を早める

       • 過学習が起きづらい

     • 参考: バッチサイズ

       • 画像系のタスクのとき、GPUなら1~64枚, TPUなら1~256枚程度

       • 2のべき乗をよく使うことが多い

実装演習

p.33 例題チャレンジ

• Q. 特徴データ datax, ラベルデータ datat に対してミニバッチを学習を行うコード例 (き) に当てはまるのは?

• A. (1)

data_x[i:i_end], data_t[i:i_end]

• こういうプログラムの虫食い問題はE資格でも結構あるらしい

初期化による勾配消失問題の改善

import sys
sys.path.append('/.')

# MLP クラス
import numpy as np
from common import layers
from collections import OrderedDict
from common import functions
from data.mnist import load_mnist
import matplotlib.pyplot as plt


class MultiLayerNet:
    '''
    input_size: 入力層のノード数
    hidden_size_list: 隠れ層のノード数のリスト
    output_size: 出力層のノード数
    activation: 活性化関数
    weight_init_std: 重みの初期化方法
    '''
    def __init__(self, input_size, hidden_size_list, output_size, activation='relu', weight_init_std='relu'):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size_list = hidden_size_list
        self.hidden_layer_num = len(hidden_size_list)
        self.params = {}

        # 重みの初期化
        self.__init_weight(weight_init_std)

        # レイヤの生成, sigmoidとreluのみ扱う
        activation_layer = {'sigmoid': layers.Sigmoid, 'relu': layers.Relu}
        self.layers = OrderedDict() # 追加した順番に格納
        for idx in range(1, self.hidden_layer_num+1):
            self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
            self.layers['Activation_function' + str(idx)] = activation_layer[activation]()

        idx = self.hidden_layer_num + 1
        self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])

        self.last_layer = layers.SoftmaxWithLoss()

    def __init_weight(self, weight_init_std):
        all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
        for idx in range(1, len(all_size_list)):
            scale = weight_init_std
            if str(weight_init_std).lower() in ('relu', 'he'):
                scale = np.sqrt(2.0 / all_size_list[idx - 1])
            elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
                scale = np.sqrt(1.0 / all_size_list[idx - 1])

            self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
            self.params['b' + str(idx)] = np.zeros(all_size_list[idx])

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, d):
        y = self.predict(x)

        weight_decay = 0
        for idx in range(1, self.hidden_layer_num + 2):
            W = self.params['W' + str(idx)]

        return self.last_layer.forward(y, d) + weight_decay

    def accuracy(self, x, d):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if d.ndim != 1 : d = np.argmax(d, axis=1)

        accuracy = np.sum(y == d) / float(x.shape[0])
        return accuracy

    def gradient(self, x, d):
        # forward
        self.loss(x, d)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 設定
        grad = {}
        for idx in range(1, self.hidden_layer_num+2):
            grad['W' + str(idx)] = self.layers['Affine' + str(idx)].dW
            grad['b' + str(idx)] = self.layers['Affine' + str(idx)].db

        return grad

def learn_and_plot(network, iters_num=2000):

    # データの読み込み
    (x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

    #iters_num = 2000
    train_size = x_train.shape[0]
    batch_size = 100
    learning_rate = 0.1

    train_loss_list = []
    accuracies_train = []
    accuracies_test = []

    plot_interval=10

    for i in range(iters_num):
        batch_mask = np.random.choice(train_size, batch_size)
        x_batch = x_train[batch_mask]
        d_batch = d_train[batch_mask]

        # 勾配
        grad = network.gradient(x_batch, d_batch)
        
        for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
            network.params[key] -= learning_rate * grad[key]
        
        loss = network.loss(x_batch, d_batch)
        train_loss_list.append(loss)
        
        if (i + 1) % plot_interval == 0:
            accr_test = network.accuracy(x_test, d_test)
            accuracies_test.append(accr_test)        
            accr_train = network.accuracy(x_batch, d_batch)
            accuracies_train.append(accr_train)
            # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
            # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
            

    lists = range(0, iters_num, plot_interval)
    plt.plot(lists, accuracies_train, label="training set")
    plt.plot(lists, accuracies_test,  label="test set")
    plt.legend(loc="lower right")
    plt.title("accuracy")
    plt.xlabel("count")
    plt.ylabel("accuracy")
    plt.ylim(0, 1.0)
    # グラフの表示
    plt.show()

# 活性化関数 と 初期化関数の組み合わせ
hidden_size_list= [40,20]

print("----------------- Sigmoid")
print("initializer: gauss")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='sigmoid', weight_init_std=0.01))

print("initializer: Xavier")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='sigmoid', weight_init_std='Xavier'))

print("initializer: He") # try
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='sigmoid', weight_init_std='He'))

print("----------------- Relu")

print("initializer: gauss")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='relu', weight_init_std=0.01))

print("initializer: Xavier") # try 
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='relu', weight_init_std='Xavier'))

print("initializer: He")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='relu', weight_init_std='He'))

----------------- Sigmoid initializer: gauss

initializer: Xavier

initializer: He

----------------- Relu initializer: gauss

initializer: Xavier

initializer: He

# 活性化関数 と 初期化関数の組み合わせ
hidden_size_list= [40,30,20]

print("----------------- Sigmoid")
print("initializer: gauss")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='sigmoid', weight_init_std=0.01),iters_num=4000)

print("initializer: Xavier")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='sigmoid', weight_init_std='Xavier'),iters_num=4000)

print("initializer: He") # try
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='sigmoid', weight_init_std='He'),iters_num=4000)

print("----------------- Relu")

print("initializer: gauss")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='relu', weight_init_std=0.01),iters_num=4000)

print("initializer: Xavier") # try 
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='relu', weight_init_std='Xavier'),iters_num=4000)

print("initializer: He")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='relu', weight_init_std='He'),iters_num=4000)

----------------- Sigmoid initializer: gauss

initializer: Xavier

initializer: He

----------------- Relu initializer: gauss

initializer: Xavier

initializer: He

• とにかく ReLU の効果が大きい

• ReLu + Xavier より 気持ち ReLU + He のほうが早い?

バッチ正規化

import sys
sys.path.append('.')

## バッチ正則化 layer の定義
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer

# バッチ正則化 layer
class BatchNormalization:
    '''
    gamma: スケール係数
    beta: オフセット
    momentum: 慣性
    running_mean: テスト時に使用する平均
    running_var: テスト時に使用する分散
    '''
    def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None):
        self.gamma = gamma
        self.beta = beta
        self.momentum = momentum
        self.input_shape = None

        self.running_mean = running_mean
        self.running_var = running_var  
        
        # backward時に使用する中間データ
        self.batch_size = None
        self.xc = None
        self.std = None
        self.dgamma = None
        self.dbeta = None

    def forward(self, x, train_flg=True):
        if self.running_mean is None:
            N, D = x.shape
            self.running_mean = np.zeros(D)
            self.running_var = np.zeros(D)
        #### batch normalization (バッチ正規化に該当する箇所)　ここから-----------------                
        if train_flg:
            mu = x.mean(axis=0) # 平均
            xc = x - mu # xをセンタリング
            var = np.mean(xc**2, axis=0) # 分散
            std = np.sqrt(var + 10e-7) # スケーリング
            xn = xc / std
            
            self.batch_size = x.shape[0]
            self.xc = xc
            self.xn = xn
            self.std = std
            self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu # 平均値の加重平均
            self.running_var = self.momentum * self.running_var + (1-self.momentum) * var #分散値の加重平均
        else:
            xc = x - self.running_mean
            xn = xc / ((np.sqrt(self.running_var + 10e-7)))
            
        out = self.gamma * xn + self.beta 
        
        return out

    def backward(self, dout):
        dbeta = dout.sum(axis=0)
        dgamma = np.sum(self.xn * dout, axis=0)
        dxn = self.gamma * dout
        dxc = dxn / self.std
        dstd = -np.sum((dxn * self.xc) / (self.std * self.std), axis=0)
        dvar = 0.5 * dstd / self.std
        dxc += (2.0 / self.batch_size) * self.xc * dvar
        dmu = np.sum(dxc, axis=0)
        dx = dxc - dmu / self.batch_size
        
        self.dgamma = dgamma
        self.dbeta = dbeta

        return dx

def learn_and_plot(network, iters_num=1000):
    (x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

    #iters_num = 1000
    train_size = x_train.shape[0]
    batch_size = 100
    learning_rate=0.01

    train_loss_list = []
    accuracies_train = []
    accuracies_test = []

    plot_interval=10


    for i in range(iters_num):
        batch_mask = np.random.choice(train_size, batch_size)
        x_batch = x_train[batch_mask]
        d_batch = d_train[batch_mask]

        grad = network.gradient(x_batch, d_batch)
        for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
            network.params[key] -= learning_rate * grad[key]

            loss = network.loss(x_batch, d_batch)
            train_loss_list.append(loss)        
            
        if (i + 1) % plot_interval == 0:
            accr_test = network.accuracy(x_test, d_test)
            accuracies_test.append(accr_test)        
            accr_train = network.accuracy(x_batch, d_batch)
            accuracies_train.append(accr_train)
            
            # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
            # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
                    

    lists = range(0, iters_num, plot_interval)
    plt.plot(lists, accuracies_train, label="training set")
    plt.plot(lists, accuracies_test,  label="test set")
    plt.legend(loc="lower right")
    plt.title("accuracy")
    plt.xlabel("count")
    plt.ylabel("accuracy")
    plt.ylim(0, 1.0)
    # グラフの表示
    plt.show()

## 元々あった状態
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10,
                        activation='sigmoid', weight_init_std='Xavier', use_batchnorm=True))

データ読み込み完了

## gauss 初期化にしたり、層の数を増やしたりして勾配消失問題が起きやすい状況をつくってみる
print("gauss 初期化で収束しにくくする")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10,
                        activation='sigmoid', weight_init_std=0.01, use_batchnorm=True))
print("さらに層を増やして勾配消失問題も起きやすくする")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=[40, 30 ,20], output_size=10,
                        activation='sigmoid', weight_init_std=0.01, use_batchnorm=True))

gauss 初期化で収束しにくくする

さらに層を増やして勾配消失問題も起きやすくする

print("He,relu,bn")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=[40, 30 ,20], output_size=10,
                        activation='relu', weight_init_std='He', use_batchnorm=True))

print("xavier,sigmoid,bn")
learn_and_plot(MultiLayerNet(input_size=784, hidden_size_list=[40, 30 ,20], output_size=10,
                        activation='sigmoid', weight_init_std='Xavier', use_batchnorm=True))

He,relu,bn

xavier,sigmoid,bn

• バッチ正則化の効果で sigmoid + gauss 初期化でもなんとか更新は進んでいるようす (でもReLUにした方が効果大きい)

• この実験のみで判断できないが、He + ReLU などで適切・十分に収束していそうなケースでは、BN入れない方が早いのかも?

2. 学習率最適化手法

• Optimizer 動作概要

  • 学習の初期の段階では、学習率大きめに設定し、徐々に学習率を小さくしていく

  • パラメータ毎に学習率を可変にする

    • パラメータ毎に学習率が変わるということは、パラメータ更新のベクトルの方向自体が変わるということ. "学習率最適化"という言葉はしっくりこないなぁ..

• 代表的な手法

  • モメンタム

    • 更新式

      • $\bm{w}^{(t+1)} = \bm{w}^{(t)} + V_t$

        • パラメータ更新量は $V_t$

      • $V_t = \mu V_{t-1} - \epsilon \nabla E$

        • $V_t$ は、勾配降下法のパラメータ更新量 $-\epsilon \nabla E$ を1次IIRをつかって Recursive average をとったもの

    • 効用

      • ささいな局所最適解につかまりにくい

      • 谷間についてから、最低値付近に収束するまでの時間が早い (しかし最終的にピタッととまりにくい)

  • AdaGrad

    • 更新式

      • $\bm{w}^{(t+1)} = \bm{w}^{(t)} - \epsilon \frac{1}{\sqrt{h_t} + \theta }\nabla E$

        • $h_t$ が大きいほど遅くなるよね

      • $h_t = h_{t-1} + (\nabla E)^2 , h_0 = \theta$

        • 最初の方は、$|\nabla E|$ で ノーマライズするような効果なので、斜面の緩急によらず速やかに収束していきそう

        • 毎回二乗で足していくので、$h_t$ は単調増加して、どんどんステップサイズは小さくなる。

    • 効用

      • 勾配の緩やかな斜面で最適値に近づいていきやすい(逆に急な斜面は不得意)

      • 鞍点問題 (SGDよりはマシなようだが..)

      • ハイパパラメータの調整が難しい

  • RMSProp

    • 鞍点問題対策を施したAdaGradの改良版

    • 更新式

      • $\bm{w}^{(t+1)} = \bm{w}^{(t)} - \epsilon \frac{1}{\sqrt{h_t} + \theta }\nabla E$

        • AdaGrad と同じ

      • $h_t = \alpha h_{t-1} + (1-\alpha) (\nabla E)^2$

        • $h_0$ の設定は AdaGrad と同じなのだろうか?

        • AdaGradで 単調増加していた $h_t$ が、単純に一個前との按分をとる形になった

    • 効用

      • AdaGradと比較して より帯域的最適解を見つけやすく、ハイパラメータの調整の難易度も下がった

  • Adam

    • モメンタムと、RMSProp のいいとこ取り版

    • 更新式 (なぜ資料にのっていないのか?!) 参考

      • $\bm{w}^{(t+1)} = \bm{w}^{(t)} - \epsilon \frac{V_t}{\sqrt{h_t} + \theta}$

      • $V_t = \mu V_{t-1} + (1-\mu) \nabla E$

      • $h_t = \alpha h_{t-1} + (1-\alpha) (\nabla E)^2$

実装演習

• Momentum をもとに AdaGrad の実装を行う

  • 講師の方、Momentum のコードが書かれているのに、AdaGrad の解説してて、コード見てないのがモロバレですよ。

• Try パート

  • 学習率増やしたら、Momenutum, AdaGrad で収束するようになったが、RMSProp, AdamがNGに,,

  • Relu, He にすると各手法よくなる

  • Batch Normalization を入れても良くなるが 活性化関数/初期化手法の方がより安定的に収束してそう?

import sys
sys.path.append('.')

import sys, os
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet

def learn_and_plot(network, optimizer="sgd", iters_num=1000, learning_rate=0.01):
    # データの読み込み
    (x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)


    train_size = x_train.shape[0]
    batch_size = 100
    # momentum 
    momentum = 0.9
    # adagrad
    theta = 1e-4
    # rmsprop
    decay_rate = 0.99
    # adam
    beta1 = 0.9
    beta2 = 0.999

    train_loss_list = []
    accuracies_train = []
    accuracies_test = []

    plot_interval=10

    for i in range(iters_num):
        batch_mask = np.random.choice(train_size, batch_size)
        x_batch = x_train[batch_mask]
        d_batch = d_train[batch_mask]

        # 勾配
        grad = network.gradient(x_batch, d_batch)
        
        if i == 0:
            if optimizer == "momentum":
                v = {} 
            elif optimizer == "adagrad" or optimizer == "rmsprop" :
                h = {}
            elif optimizer == "adam":
                m = {}
                v = {} 
        

        for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
            if optimizer == "sgd":
                network.params[key] -= learning_rate * grad[key]
            elif optimizer == "momentum":
                if i == 0:
                    v[key] = np.zeros_like(network.params[key]) 
                v[key] = momentum * v[key] - learning_rate * grad[key]
                network.params[key] += v[key]
            elif optimizer == "adagrad":
                if i == 0:
                    h[key] = np.full_like(network.params[key],theta)
                h[key] = h[key] + np.square(grad[key]) 
                network.params[key] -= learning_rate / np.sqrt(h[key]) * grad[key]
            elif optimizer == "rmsprop":
                if i == 0:
                    h[key] = np.zeros_like(network.params[key])
                h[key] *= decay_rate
                h[key] += (1-decay_rate) * np.square(grad[key]) 
                network.params[key] -= learning_rate * grad[key] / (np.sqrt(h[key]) + 1e-7) 
            elif optimizer == "adam":
                if i == 0:
                    m[key] = np.zeros_like(network.params[key])
                    v[key] = np.zeros_like(network.params[key])

                m[key] += (1-beta1) * (grad[key] - m[key])
                v[key] += (1-beta2) * (grad[key]**2 - v[key])

                network.params[key] -= learning_rate * m[key] / (np.sqrt(v[key]) + 1e-7) 

            loss = network.loss(x_batch, d_batch)
            train_loss_list.append(loss)
        
        
        if (i + 1) % plot_interval == 0:
            accr_test = network.accuracy(x_test, d_test)
            accuracies_test.append(accr_test)        
            accr_train = network.accuracy(x_batch, d_batch)
            accuracies_train.append(accr_train)
            
            # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
            # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))

            
    lists = range(0, iters_num, plot_interval)
    plt.plot(lists, accuracies_train, label="training set")
    plt.plot(lists, accuracies_test,  label="test set")
    plt.legend(loc="lower right")
    plt.title("accuracy")
    plt.xlabel("count")
    plt.ylabel("accuracy")
    plt.ylim(0, 1.0)
    # グラフの表示
    plt.show()

# default 状態
iters_num = 1000
activation = "sigmoid"
initiazlier = 0.01
use_batchnorm = False

optimizer_list = ["sgd", "momentum", "adagrad", "adagrad", "rmsprop", "adam"]

for optimizer in optimizer_list:
    print(optimizer)
    network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation=activation, weight_init_std=initiazlier,
                        use_batchnorm=use_batchnorm)
    learn_and_plot(network,optimizer, iters_num)

sgd

momentum

adagrad

rmsprop

adam

# 学習率を増やしてみる 0.01 -> 0.1 
iters_num = 1000
activation = "sigmoid"
learning_rate = 0.1
initiazlier = 0.01
use_batchnorm = False

optimizer_list = ["sgd", "momentum", "adagrad", "adagrad", "rmsprop", "adam"]

for optimizer in optimizer_list:
    print(optimizer)
    network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation=activation, weight_init_std=initiazlier,
                        use_batchnorm=use_batchnorm)
    learn_and_plot(network,optimizer, iters_num,learning_rate)

sgd

momentum

adagrad

rmsprop

adam

# デフォルト状態から 活性化関数を
iters_num = 1000
activation = "relu"
initiazlier = 0.01
use_batchnorm = False

optimizer_list = ["sgd", "momentum", "adagrad", "adagrad", "rmsprop", "adam"]

for optimizer in optimizer_list:
    print(optimizer)
    network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation=activation, weight_init_std=initiazlier,
                        use_batchnorm=use_batchnorm)
    learn_and_plot(network,optimizer, iters_num)

sgd

momentum

adagrad

adagrad

rmsprop

adam

# さらに初期化を He へ
iters_num = 1000
activation = "relu"
initiazlier = "He"
use_batchnorm = False

optimizer_list = ["sgd", "momentum", "adagrad", "adagrad", "rmsprop", "adam"]

for optimizer in optimizer_list:
    print(optimizer)
    network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation=activation, weight_init_std=initiazlier,
                        use_batchnorm=use_batchnorm)
    learn_and_plot(network,optimizer, iters_num)

sgd

momentum

adagrad

adagrad

rmsprop

adam

# すでにひとつ前の状態でどの手法でもある程度収束しているので、
# BNいれても変化が見つけづらそう? -> 活性化関数・初期化手法を戻して BN入れて見る
iters_num = 1000
activation = "sigmoid"
initiazlier = 0.01
use_batchnorm = True

optimizer_list = ["sgd", "momentum", "adagrad", "adagrad", "rmsprop", "adam"]

for optimizer in optimizer_list:
    print(optimizer)
    network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation=activation, weight_init_std=initiazlier,
                        use_batchnorm=use_batchnorm)
    learn_and_plot(network,optimizer, iters_num)

sgd

momentum

adagrad

adagrad

rmsprop

adam

3. 過学習

• Day1 の 13_過学習 の動画の内容

  • 機械学習の項でやった内容なので、詳細割愛

  • 過学習はパラメータ数の大きい巨大なモデルだと容易に起こる

• 過学習

  • データに対してはうまくいくが、テストデータに対してうまくいかない減少

    • 特定の訓練サンプルに特化した振る舞いを学習されてしまっている

    • 訓練誤差は下がるが、テスト誤差が下がらない(悪化する)

  • 原因

    • 訓練データの次元数・サンプル数に対して、ネットワークの自由度が高すぎる

  • 対策

    • early stopping

      • 学習曲線をプロットして訓練誤差とテスト誤差が乖離し始める前のエポックのパラメータを採用する

    • 正則化

      • 着眼点: 過学習のときは特定のサンプルの特徴が過大評価されているため重みが大きくなりがち

        • -> 重みの大きさを下げるような制約をモデルに課せばよい

      • 具体例

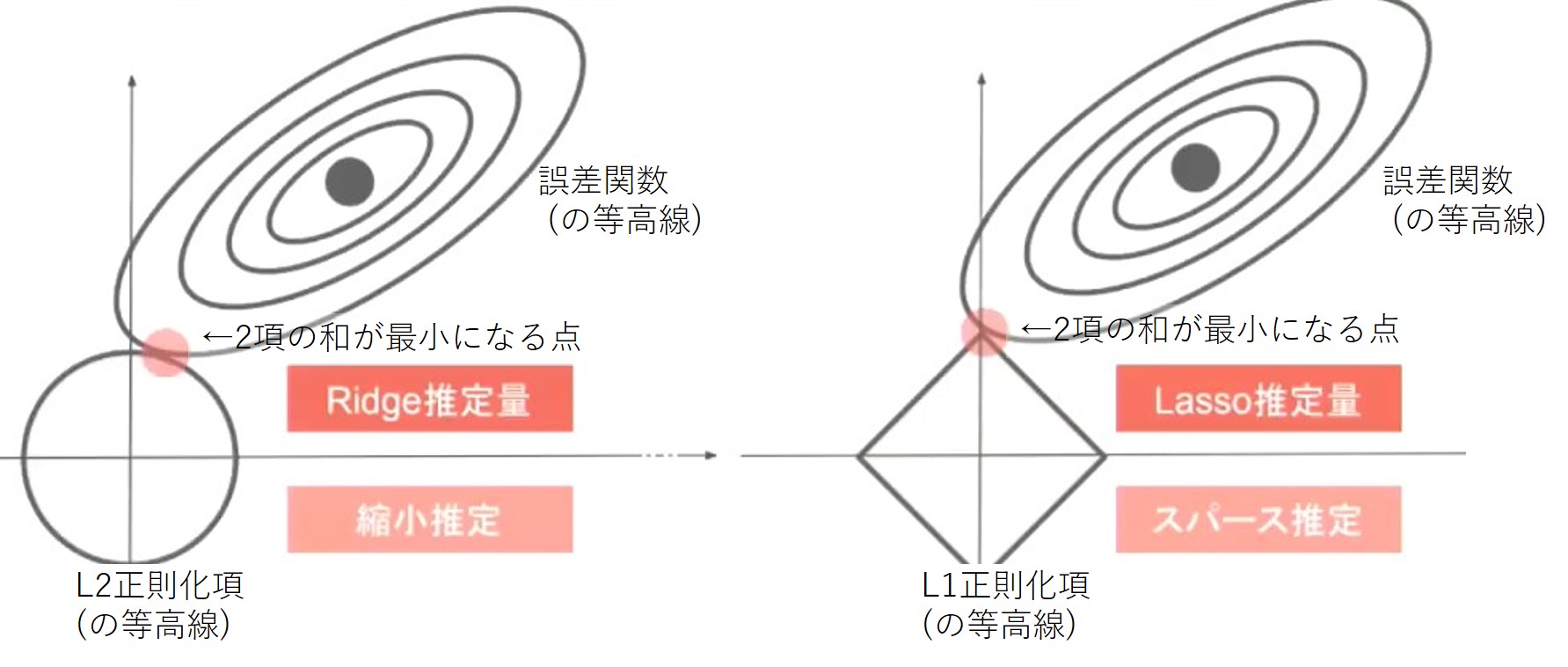
        • L1正則化 (Lasso回帰)

          • 重みベクトルの1ノルム(マンハッタン距離) の総和を正則化項として目的関数に足す

            • スパース化

            • 

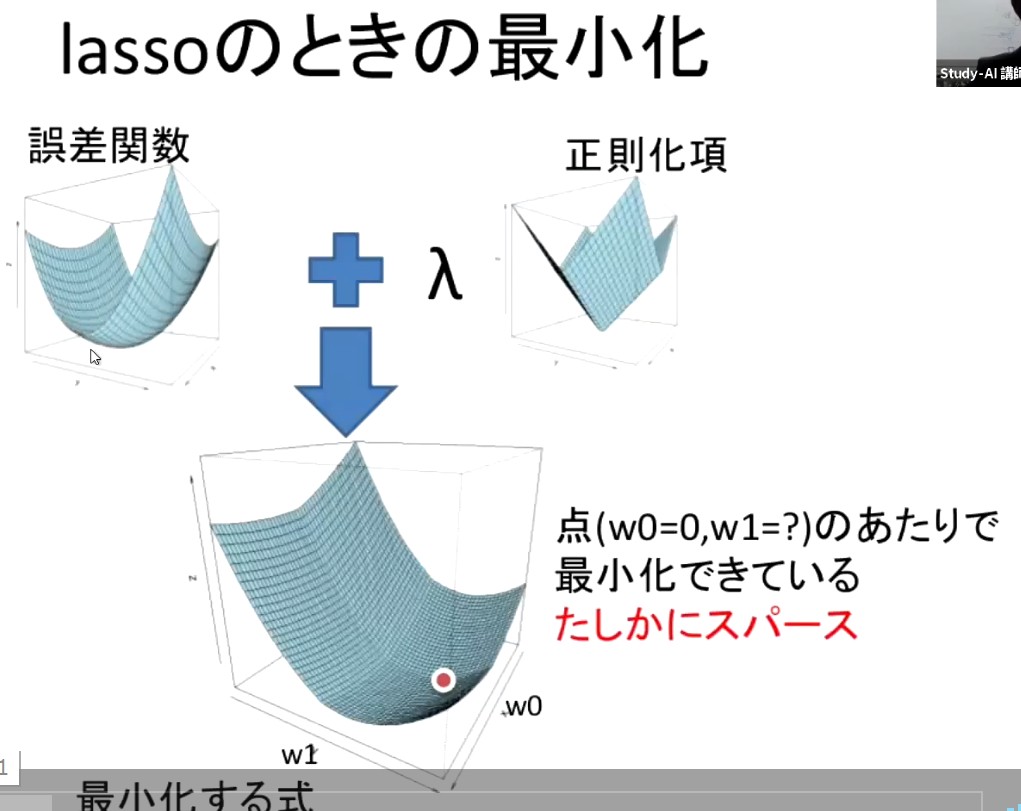
        • L2正則化 (Ridge回帰)

          • 重みベクトルの2ノルム(ユークリッド距離) の総和を正則化項として目的関数に足す

            • 全体として原点に近い位置に目的関数の谷底をシフト

            • 

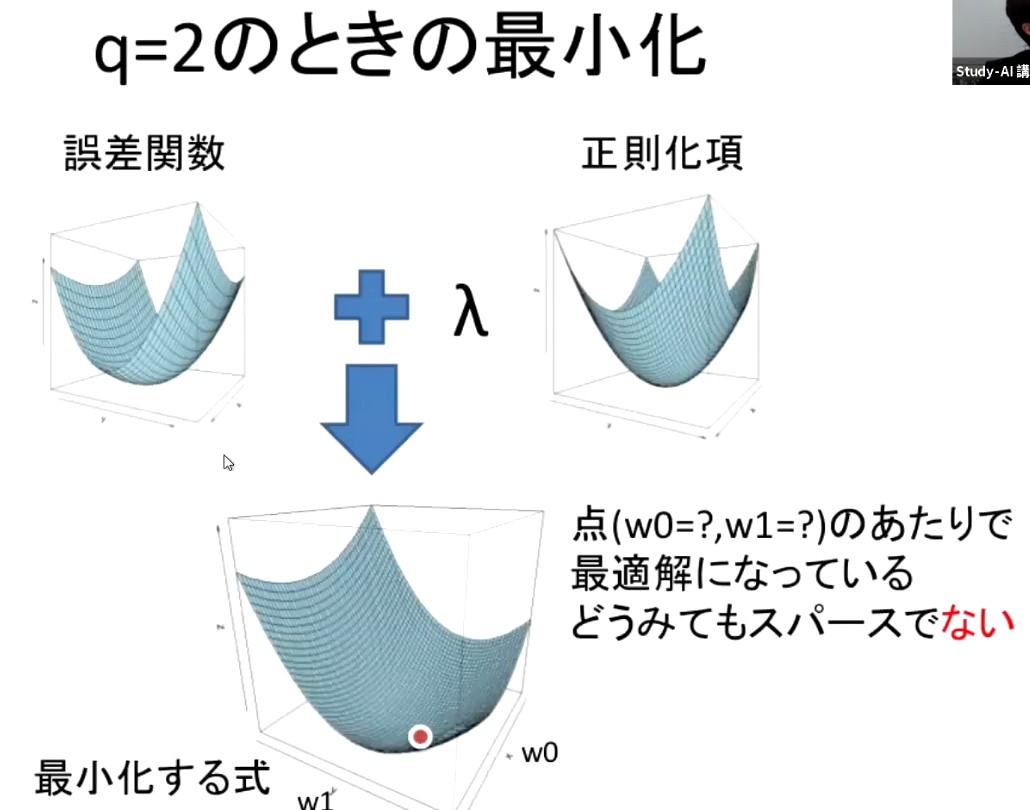
      • (確認テスト:3-1) Lassoは下図右側

        • 

    • ドロップアウト

      • 学習のパラメータ更新のたびに、ランダムにノードを削除する

      • データにバリエーションを与えているようなもの

実装演習

例題チャレンジ

L2正則化の勾配計算

def ridge(param, grad, rate):
  """
  param: target parameter
  grad: gradients to param
  rate: ridge coefficient
  """
  grad += rate * param # <- ココ (4)

L1正則化の勾配計算

def lasso(param, grad, rate):
  """
  param: target parameter
  grad: gradients to param
  rate: lasso coefficient
  """    
  x = sign(param) # <-ココ (3)
  grad += rate * x

overfitting

import sys
sys.path.append('.')

import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer

パラメータを変えてなんども試すので、関数化しておく。

• regulation 引数で、正則化 なし、L1,L2 を切り替える

• 正則化ありのパラメータ更新は勉強のために、オリジナルのコードと同じくベタで書いている (OptimizerはSDG前提のパラメータ更新)

• network 生成時の 引数を変えることで、dropout true/false, ratio 他も変更可能

def train(network, optimizer_obj, learning_rate, weight_decay_lambda = 0.0, regulation=None,  iters_num = 1000 ):
    (x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
    # print("データ読み込み完了")

    # 過学習を再現するために、学習データを削減
    x_train = x_train[:300]
    d_train = d_train[:300]

    #iters_num = 1000
    train_size = x_train.shape[0]
    batch_size = 100

    train_loss_list = []
    accuracies_train = []
    accuracies_test = []

    plot_interval=10

    for i in range(iters_num):
        batch_mask = np.random.choice(train_size, batch_size)
        x_batch = x_train[batch_mask]
        d_batch = d_train[batch_mask]

        grad = network.gradient(x_batch, d_batch)
        loss = 0
        if regulation == None:
            optimizer_obj.update(network.params, grad)
        elif regulation == 'L2':
            weight_decay = 0
            for idx in range(1, network.hidden_layer_num+1):
                grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
                grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
                network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
                network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
                # weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2)) # こうかかれていたが..
                weight_decay += 0.5 * weight_decay_lambda * np.sum(network.params['W' + str(idx)] ** 2) # こっちじゃないか?
            loss = weight_decay 
        elif regulation == 'L1':
            weight_decay = 0
            for idx in range(1, network.hidden_layer_num+1):
                grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
                grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
                network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
                network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
                weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))

            loss = weight_decay            
        
        loss = loss + network.loss(x_batch, d_batch)
        train_loss_list.append(loss)
            
        if (i+1) % plot_interval == 0:
            accr_train = network.accuracy(x_train, d_train)
            accr_test = network.accuracy(x_test, d_test)
            accuracies_train.append(accr_train)
            accuracies_test.append(accr_test)

            # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
            # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))        

    lists = range(0, iters_num, plot_interval)
    plt.plot(lists, accuracies_train, label="training set")
    plt.plot(lists, accuracies_test,  label="test set")
    plt.legend(loc="lower right")
    plt.title("accuracy")
    plt.xlabel("count")
    plt.ylabel("accuracy")
    plt.ylim(0, 1.0)
    # グラフの表示
    plt.show()

基準となる 正則化無し, Dropout無し, SDGの場合は訓練データの正解率100%に対して 検証データの正解率75%程度。かなり結果に差があり過学習が起きていると思われる

# 正則化無し, Dropout 無し
learning_rate = 0.01
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer_obj = optimizer.SGD(learning_rate=learning_rate)

train(network,optimizer_obj,learning_rate)

L2正則化の重みを変えてみると、0.01では小さすぎ(正則化無しとほぼ変わらない)、1.0 は大きすぎ。 その間で探すと、そこそこの結果っぽくはなるが、これでいいのかはちょっとわからない。

# L2 

lambda_list = [0.01, 0.08, 1.0]
learning_rate = 0.01
regulation = 'L2'
iters_num = 1000

for weight_decay_lambda in lambda_list:
    print(weight_decay_lambda)
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
    optimizer_obj = optimizer.SGD(learning_rate=learning_rate)
    train(network,optimizer_obj,learning_rate,weight_decay_lambda, regulation,iters_num=iters_num)

0.01

0.08

1.0

L1正則化。与えられたコードでは、学習率が0.1 だったが、L2正則化と合わせて 0.01にした。 元のloss関数も、学習に使うデータも変わらないのだし、正則化項とのバランスは weightdecaylambda 使えばいいので、 そちらのほうが、振舞いなども比較しやすいだろう。

L2正則化と似たような結果が得られる。講義動画でグラフがバタついてたのは L1正則化を使っていたこと「だけ」が原因でなく、その時の学習率が大きすぎて必要以上に0重みが増えたり減ったりしていたからでは?

# L1
lambda_list = [0.0005, 0.008, 0.05]
learning_rate = 0.01
regulation = 'L1'
iters_num = 1000

for weight_decay_lambda in lambda_list:
    print(weight_decay_lambda)
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
    optimizer_obj = optimizer.SGD(learning_rate=learning_rate)
    train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation, iters_num)

0.0005

0.008

0.05

class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None

    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio) # ランダム要素をいれない分、学習時に有効なノードの割合をかけて辻褄合わせる?

    def backward(self, dout):
        return dout * self.mask

Dropout. SGD で、正則化無。

講義動画では、「うまくいっている」風なことが言われていたが、イタレーションを増やすと、ただ収束がゆっくりになっただけで、訓練データは正解率100% に到達する。 最終的には過学習してしまっているのではないか？という気もするが、たとえば、dropout ratio 0.2 のケースで、early stopping を前提にすると、検証データの正解率がサチリかけたときに、訓練データの正解率がまだ、100%に達しておらず、ワンチャン絶妙なモデルが得られるかもしれない?

# common settings 
use_dropout = True
weight_decay_lambda = 0
regulation = None
learning_rate = 0.01
dropout_ratio_list = [0.15, 0.2, 0.3, 0.4]
iters_num_list    = [3000, 4000, 5000, 6000]

for i in range(len(dropout_ratio_list)):
    dropout_ratio = dropout_ratio_list[i]
    print(dropout_ratio)
    iters_num = iters_num_list[i]
    optimizer_obj = optimizer.SGD(learning_rate=learning_rate)
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                            use_dropout = use_dropout, dropout_ratio = dropout_ratio)
    train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation,iters_num)

0.15

0.2

0.3

0.4

dropout ratio 0, 0.15, 0.2 で各種 optimizer を試してみる。正則化はとりあえずなし そもそもdroptout 無しの状態で、SGDと比べて、収束早い & 検証データの成果率が若干高い。 Droptout有りのときもあまり収束がSlowDownしないし、訓練データはすぐに正解率100%になる。これをどう捉えるべきか?

# common settings 
use_dropout = True
weight_decay_lambda = 0
regulation = None
learning_rate = 0.01
dropout_ratio_list = [0, 0.15, 0.2]
iters_num_list    = [1000, 3000, 4000]

# -------------------------------------------------------
print("Momentum+Droptout")
for i in range(len(dropout_ratio_list)):
    dropout_ratio = dropout_ratio_list[i]
    print(dropout_ratio)
    iters_num = iters_num_list[i]
    optimizer_obj = optimizer.Momentum(learning_rate=learning_rate,momentum=0.9)
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                            use_dropout = use_dropout, dropout_ratio = dropout_ratio)
    train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation,iters_num)
# -------------------------------------------------------
print("AdaGrad+Droptout")
for i in range(len(dropout_ratio_list)):
    dropout_ratio = dropout_ratio_list[i]
    print(dropout_ratio)
    iters_num = iters_num_list[i]
    optimizer_obj = optimizer.AdaGrad(learning_rate=learning_rate)
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                            use_dropout = use_dropout, dropout_ratio = dropout_ratio)
    train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation,iters_num)
# -------------------------------------------------------
print("Adam+Droptout")
for i in range(len(dropout_ratio_list)):
    dropout_ratio = dropout_ratio_list[i]
    print(dropout_ratio)
    iters_num = iters_num_list[i]
    optimizer_obj = optimizer.Adam()
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                            use_dropout = use_dropout, dropout_ratio = dropout_ratio)
    train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation,iters_num)

Momentum+Droptout 0

0.15

0.2

AdaGrad+Droptout 0

0.15

0.2

Adam+Droptout 0

0.15

0.2

Dropout (ratio 0.1) + L2 正則化。 最初に実装したtrain関数は、正則化を行う時のパラメータ更新のコードがSGD前提になってしまっている。 各種Optimizer 全部ためすのは面倒だなぁと思っていたが、multilayernet.py のコードを見ると、 実はnetwork生成時に、weight decay lambda の数値を与えると、コスト関数に 重み係数の二乗和が追加されるので、L2正則化っぽいことが試せる.

(ちなみに、デフォルトのコードでは、Droptouのコード例で、このweightdecaylambda が network 生成時に与えられているので、何も考えずに頭から実行した場合は、実は、L1正則化単体の実験で使われていた、weightdecaylambda = 0.005 が使われることになるのだが、コードを準備した方の意図通りだろうか?)

# common settings 
use_dropout = True
weight_decay_lambda = 0.05
regulation = None
learning_rate = 0.01
dropout_ratio = 0.08
iters_num    = 2000

#------------------------------------------------------------
print("SGD+Droptout+L2")
optimizer_obj = optimizer.SGD(learning_rate=learning_rate)
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda,use_dropout = use_dropout, dropout_ratio = dropout_ratio)
train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation,iters_num)

# -------------------------------------------------------
print("Momentum+Droptout+L2")
optimizer_obj = optimizer.Momentum(learning_rate=learning_rate, momentum=0.9)
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda,  use_dropout = use_dropout, dropout_ratio = dropout_ratio)
train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation,iters_num)

# -------------------------------------------------------
print("AdaGrad+Droptout+L2")
optimizer_obj = optimizer.AdaGrad(learning_rate=learning_rate)
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda, use_dropout = use_dropout, dropout_ratio = dropout_ratio)
train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation,iters_num)
# -------------------------------------------------------
print("Adam+Droptout+L2")
optimizer_obj = optimizer.Adam()
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda, use_dropout = use_dropout, dropout_ratio = dropout_ratio)
train(network, optimizer_obj, learning_rate, weight_decay_lambda, regulation,iters_num)

SGD+Droptout+L2

Momentum+Droptout+L2

AdaGrad+Droptout+L2

Adam+Droptout+L2

SGDで Dropout + L1 正則化。反復回数だけ増やして実行。 1000回まではよさげにみえたが、その後は、訓練データは微増に対して、検証データは微減。このケースの場合は 1000回ちょっと手前くらいで止めておこうということになるのかな?

from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

print("データ読み込み完了")

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]

# ドロップアウト設定 ======================================
use_dropout = True
dropout_ratio = 0.08
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        use_dropout = use_dropout, dropout_ratio = dropout_ratio)

iters_num = 3000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01

train_loss_list = []
accuracies_train = []
accuracies_test = []
hidden_layer_num = network.hidden_layer_num

plot_interval=10

# 正則化強度設定 ======================================
weight_decay_lambda=0.004
# =================================================

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    grad = network.gradient(x_batch, d_batch)
    weight_decay = 0
    
    for idx in range(1, hidden_layer_num+1):
        grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
        grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
        network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
        network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
        weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))

    loss = network.loss(x_batch, d_batch) + weight_decay
    train_loss_list.append(loss)        
        
    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)
        
        # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))               
        
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()

データ読み込み完了

4. 畳み込みニューラルネットワーク(CNN)の概念

• CNN で扱うデータ

  • Day1 "15CNNで扱えるデータの種類" & Day2 "21CNN -構造1" の動画 共通の内容

  • CNNで扱うと有効なデータ = 次元間でのつながりに意味があるデータ

    • 例:

      • 単一チャンネル 音声(1次元)、スペクトログラム画像(2次元),　CTスキャン画像(3次元)

      • 複数チャンネル アニメのスケルトン(1次元), カラー画像(2次元), 動画(3次元)

• CNN の構造

  • 全体の把握: LeNet を例に 各層におけるデータサイズに着目して概要ざっくり説明

    • 入力 : 32 x 32 = 1024 の白黒画像

    • 特徴量の抽出: 次元のつながりを保つ

    • C1: 28x28x6 = 4704 (6人の人に28x28のサイズで感想を聞いた)

    • S2: 14x14x6 = 1176 (6人の感想それぞれを 14x14 に要約)

    • C3: 10x10x16 = 1600 (要約された6人の感想を16人の人に読んでもらって、それぞれに感想を言ってもらう)

    • S4: 5x 5x16 = 400 (16人それぞれの感想を 5x5のサイズに要約)

    • 欲しい形式のデータに変換:

    • C5~ : 全結合層

    • 出力 : 10次元ベクトル(分類クラスのホットエンコーディングかな?)

  • 畳み込み層 (Convolution Layer) の演算

    • 画像の場合, 縦、横, チャンネル の3次元データに対して行う

    • 畳み込み演算

      • フィルター処理: (重み) を使った畳み込み計算 (数式上は相関計算)

        • (動画では言及がなかったが)　入力チャンネル数分だけ別々のフィルタを書けて、フィルタ処理後の値は加算する.

      • バイアス: フィルター処理の出力の各画素に、バイアスを足す

      • パディング: フィルター処理まえに上下左右に n ピクセルずつ広げて、それを入力画像として使う

        • 畳み込み層を重ねるたびに、画像サイズがどんどん小さくなるのを防ぐ

      • ストライド: フィルタ処理の際のホップサイズ

      • プーリング層: フィルタ処理のように演算対象範囲をずらしながら、演算を行う

        • Max Pooling　: 最大値をとってくる

        • Average Pooling : 範囲内の値の平均をとる

      • (出力)チャンネル : 上記までに説明された処理を、同じ入力に対して別々のフィルタを使って行う

    • (確認テスト:4-1) 6x6の画像に2x2のフィルタを畳み込む、ストライド・パディングは1, 出力サイズは?

      • answer : 7x7

        • パディング後のサイズ (size 6) + (padding 1) * 2 = 8

        • 一番右端にフィルタをかける時、フィルタの左端の位置は 8 - ( (kernel size 2) -1) = 7

        • ストライド 1 なので、 7/ (stride 1) = 7

        • dilation があるともうちょっと複雑

      • 疑問点:

        • ストライド 2 以上にしたとき、割り切れない場合はどうするの?

        • PyTorchの実装ではマニュアル みると切り落としっぽい。

• 畳み込み処理の実装演習

  • フィルタ処理のメモリアクセスは効率が悪いので、dot積でフィルタ処理ができるようなデータに並び替える(冗長になる)

    • 実装演習の image2col のパート参照

    • kernelsize 2 なら、2x2=4 つのデータを一列(or一行)に kernelsize 3 なら 3x3=9つのデータを一列に。

実装演習: 畳み込みレイヤーの実装例

• im2col : forward 計算で使用。上述の通り 畳み込み処理を np.dot() を使って効率よく行うために、入力データとフィルタの変換を行う

• col2im : backward 計算で 誤差逆伝播を計算するときにつかう。基本的にはim2col の逆変換のようなことをするのだが、入力のある画素のデータに起因した誤差が、col形式では、各列に分散されているので、それらを足し合わせる必要がある。

import pickle
import numpy as np
from collections import OrderedDict
from common import layers
from common import optimizer
from data.mnist import load_mnist
import matplotlib.pyplot as plt

import sys
sys.path.append('.')

効率よく行列計算をするためのデータ変換

im2col <-> col2im の実装

'''
input_data/col : 畳み込み層への入力データ / 変換後データ
filter_h: フィルターの高さ
filter_w: フィルターの横幅
stride: ストライド
pad: パディング
'''
# 画像データを２次元配列に変換
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    # N: number, C: channel, H: height, W: width
    N, C, H, W = input_data.shape
    out_h = (H + 2 * pad - filter_h)//stride + 1
    out_w = (W + 2 * pad - filter_w)//stride + 1

    img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

    for y in range(filter_h):
        y_max = y + stride * out_h
        for x in range(filter_w):
            x_max = x + stride * out_w
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
    
    col = col.transpose(0, 4, 5, 1, 2, 3) # (N, C, filter_h, filter_w, out_h, out_w) -> (N, filter_w, out_h, out_w, C, filter_h)    
    
    col = col.reshape(N * out_h * out_w, -1)
    return col

# ２次元配列を画像データに変換
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    # N: number, C: channel, H: height, W: width
    N, C, H, W = input_shape
    # 切り捨て除算    
    out_h = (H + 2 * pad - filter_h)//stride + 1
    out_w = (W + 2 * pad - filter_w)//stride + 1
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2) # (N, filter_h, filter_w, out_h, out_w, C)

    img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
    for y in range(filter_h):
        y_max = y + stride * out_h
        for x in range(filter_w):
            x_max = x + stride * out_w
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

    return img[:, :, pad:H + pad, pad:W + pad]

def print_im2col_col2im(input_data, conv_param):
    filter_h, filter_w, stride, pad = conv_param
    print('====== input_data =======\n', input_data)
    print('==========================')
    col = im2col(input_data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
    print('========= im2col ==========\n', col)
    print('=========================')

    img = col2im(col, input_shape=input_data.shape, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
    print('========= col2im ==========\n', img)
    print('=========================')
    print()

im2col の振舞いを理解するため、(わかりやすさのため)全要素1の入力を考える 2x2 のフィルタだと、col2im の結果は

• stride = 2 にすればオーバーラップがなくなるため、全部 1 になる

• padding = 1 にすれば全画素が同じだけ使用されて、全部 4 になる

うん。納得。

input_data = np.reshape(np.ones(16), (1, 1, 4, 4)) # number, channel, height, widthを表す

conv_param =  (2,2,1,0)  # filter_h, filter_w, stride, pad
print("filter_h, fitler_w, stride, padding = ", conv_param)
print_im2col_col2im( input_data , conv_param)

conv_param =  (2,2,2,0) # filter_h, filter_w, stride, pad
print("filter_h, fitler_w, stride, padding = ", conv_param)
print_im2col_col2im( input_data , conv_param)


conv_param =  (2,2,1,2) # filter_h, filter_w, stride, pad
print("filter_h, fitler_w, stride, padding = ", conv_param)
print_im2col_col2im( input_data , conv_param)



# input_data = np.random.rand(2, 1, 4, 4)*100//1 # number, channel, height, widthを表す

filter_h, fitler_w, stride, padding =  (2, 2, 1, 0)
    ====== input_data =======
     [[[[1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]]]]
    ==========================
    ========= im2col ==========
     [[1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]]
    =========================
    ========= col2im ==========
     [[[[1. 2. 2. 1.]
       [2. 4. 4. 2.]
       [2. 4. 4. 2.]
       [1. 2. 2. 1.]]]]
    =========================
    
    filter_h, fitler_w, stride, padding =  (2, 2, 2, 0)
    ====== input_data =======
     [[[[1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]]]]
    ==========================
    ========= im2col ==========
     [[1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]]
    =========================
    ========= col2im ==========
     [[[[1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]]]]
    =========================
    
    filter_h, fitler_w, stride, padding =  (2, 2, 1, 2)
    ====== input_data =======
     [[[[1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]]]]
    ==========================
    ========= im2col ==========
     [[0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 1.]
     [0. 0. 1. 1.]
     [0. 0. 1. 1.]
     [0. 0. 1. 1.]
     [0. 0. 1. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 1. 0. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 0. 1. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 1. 0. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 0. 1. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 1. 0. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 1. 1. 1.]
     [1. 0. 1. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 1. 0. 0.]
     [1. 1. 0. 0.]
     [1. 1. 0. 0.]
     [1. 1. 0. 0.]
     [1. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]
     [0. 0. 0. 0.]]
    =========================
    ========= col2im ==========
     [[[[4. 4. 4. 4.]
       [4. 4. 4. 4.]
       [4. 4. 4. 4.]
       [4. 4. 4. 4.]]]]
    =========================

そのほかのデータ構造でも試してみる。 ( im2col までは ) 通し番号の方がわかりやすいので randでなくrangeをつかう。

input_data = np.reshape(range(100), (2, 2, 5, 5)) # number, channel, height, widthを表す

conv_param =  (3,3,2,1)  # filter_h, filter_w, stride, pad
print("filter_h, fitler_w, stride, padding = ", conv_param)
print_im2col_col2im( input_data , conv_param)

filter_h, fitler_w, stride, padding =  (3, 3, 2, 1)
    ====== input_data =======
     [[[[ 0  1  2  3  4]
       [ 5  6  7  8  9]
       [10 11 12 13 14]
       [15 16 17 18 19]
       [20 21 22 23 24]]
    
      [[25 26 27 28 29]
       [30 31 32 33 34]
       [35 36 37 38 39]
       [40 41 42 43 44]
       [45 46 47 48 49]]]
    
    
     [[[50 51 52 53 54]
       [55 56 57 58 59]
       [60 61 62 63 64]
       [65 66 67 68 69]
       [70 71 72 73 74]]
    
      [[75 76 77 78 79]
       [80 81 82 83 84]
       [85 86 87 88 89]
       [90 91 92 93 94]
       [95 96 97 98 99]]]]
    ==========================
    ========= im2col ==========
     [[ 0.  0.  0.  0.  0.  1.  0.  5.  6.  0.  0.  0.  0. 25. 26.  0. 30. 31.]
     [ 0.  0.  0.  1.  2.  3.  6.  7.  8.  0.  0.  0. 26. 27. 28. 31. 32. 33.]
     [ 0.  0.  0.  3.  4.  0.  8.  9.  0.  0.  0.  0. 28. 29.  0. 33. 34.  0.]
     [ 0.  5.  6.  0. 10. 11.  0. 15. 16.  0. 30. 31.  0. 35. 36.  0. 40. 41.]
     [ 6.  7.  8. 11. 12. 13. 16. 17. 18. 31. 32. 33. 36. 37. 38. 41. 42. 43.]
     [ 8.  9.  0. 13. 14.  0. 18. 19.  0. 33. 34.  0. 38. 39.  0. 43. 44.  0.]
     [ 0. 15. 16.  0. 20. 21.  0.  0.  0.  0. 40. 41.  0. 45. 46.  0.  0.  0.]
     [16. 17. 18. 21. 22. 23.  0.  0.  0. 41. 42. 43. 46. 47. 48.  0.  0.  0.]
     [18. 19.  0. 23. 24.  0.  0.  0.  0. 43. 44.  0. 48. 49.  0.  0.  0.  0.]
     [ 0.  0.  0.  0. 50. 51.  0. 55. 56.  0.  0.  0.  0. 75. 76.  0. 80. 81.]
     [ 0.  0.  0. 51. 52. 53. 56. 57. 58.  0.  0.  0. 76. 77. 78. 81. 82. 83.]
     [ 0.  0.  0. 53. 54.  0. 58. 59.  0.  0.  0.  0. 78. 79.  0. 83. 84.  0.]
     [ 0. 55. 56.  0. 60. 61.  0. 65. 66.  0. 80. 81.  0. 85. 86.  0. 90. 91.]
     [56. 57. 58. 61. 62. 63. 66. 67. 68. 81. 82. 83. 86. 87. 88. 91. 92. 93.]
     [58. 59.  0. 63. 64.  0. 68. 69.  0. 83. 84.  0. 88. 89.  0. 93. 94.  0.]
     [ 0. 65. 66.  0. 70. 71.  0.  0.  0.  0. 90. 91.  0. 95. 96.  0.  0.  0.]
     [66. 67. 68. 71. 72. 73.  0.  0.  0. 91. 92. 93. 96. 97. 98.  0.  0.  0.]
     [68. 69.  0. 73. 74.  0.  0.  0.  0. 93. 94.  0. 98. 99.  0.  0.  0.  0.]]
    =========================
    ========= col2im ==========
     [[[[  0.   2.   2.   6.   4.]
       [ 10.  24.  14.  32.  18.]
       [ 10.  22.  12.  26.  14.]
       [ 30.  64.  34.  72.  38.]
       [ 20.  42.  22.  46.  24.]]
    
      [[ 25.  52.  27.  56.  29.]
       [ 60. 124.  64. 132.  68.]
       [ 35.  72.  37.  76.  39.]
       [ 80. 164.  84. 172.  88.]
       [ 45.  92.  47.  96.  49.]]]
    
    
     [[[ 50. 102.  52. 106.  54.]
       [110. 224. 114. 232. 118.]
       [ 60. 122.  62. 126.  64.]
       [130. 264. 134. 272. 138.]
       [ 70. 142.  72. 146.  74.]]
    
      [[ 75. 152.  77. 156.  79.]
       [160. 324. 164. 332. 168.]
       [ 85. 172.  87. 176.  89.]
       [180. 364. 184. 372. 188.]
       [ 95. 192.  97. 196.  99.]]]]
    =========================

class Convolution:
    # W: フィルター, b: バイアス
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
        
        # 中間データ（backward時に使用）
        self.x = None   
        self.col = None
        self.col_W = None
        
        # フィルター・バイアスパラメータの勾配
        self.dW = None
        self.db = None

    def forward(self, x):
        # FN: filter_number, C: channel, FH: filter_height, FW: filter_width
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        # 出力値のheight, width
        out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
        out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)
        
        # xを行列に変換
        col = im2col(x, FH, FW, self.stride, self.pad)
        # フィルターをxに合わせた行列に変換
        col_W = self.W.reshape(FN, -1).T

        out = np.dot(col, col_W) + self.b
        # 計算のために変えた形式を戻す
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

        self.x = x
        self.col = col
        self.col_W = col_W

        return out

    def backward(self, dout):
        FN, C, FH, FW = self.W.shape
        dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)

        self.db = np.sum(dout, axis=0)
        self.dW = np.dot(self.col.T, dout)
        self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)

        dcol = np.dot(dout, self.col_W.T)
        # dcolを画像データに変換
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)

        return dx

    
class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad
        
        self.x = None
        self.arg_max = None

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)
        
        # xを行列に変換
        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
        # プーリングのサイズに合わせてリサイズ
        col = col.reshape(-1, self.pool_h*self.pool_w)
        
        # 行ごとに最大値を求める
        arg_max = np.argmax(col, axis=1)
        out = np.max(col, axis=1)
        # 整形
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)

        self.x = x
        self.arg_max = arg_max

        return out

    def backward(self, dout):
        dout = dout.transpose(0, 2, 3, 1)
        
        pool_size = self.pool_h * self.pool_w
        dmax = np.zeros((dout.size, pool_size))
        dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
        dmax = dmax.reshape(dout.shape + (pool_size,)) 
        
        dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
        dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
        
        return dx

# simple CNN の実装・学習例

class SimpleConvNet:
    # conv - relu - pool - affine - relu - affine - softmax
    def __init__(self, input_dim=(1, 28, 28), conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
                 hidden_size=100, output_size=10, weight_init_std=0.01):
        filter_num = conv_param['filter_num']        
        filter_size = conv_param['filter_size']
        filter_pad = conv_param['pad']
        filter_stride = conv_param['stride']
        input_size = input_dim[1]
        conv_output_size = (input_size - filter_size + 2 * filter_pad) / filter_stride + 1
        pool_output_size = int(filter_num * (conv_output_size / 2) * (conv_output_size / 2))

        # 重みの初期化
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
        self.params['b1'] = np.zeros(filter_num)
        self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        # レイヤの生成
        self.layers = OrderedDict()
        self.layers['Conv1'] = layers.Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad'])
        self.layers['Relu1'] = layers.Relu()
        self.layers['Pool1'] = layers.Pooling(pool_h=2, pool_w=2, stride=2)
        self.layers['Affine1'] = layers.Affine(self.params['W2'], self.params['b2'])
        self.layers['Relu2'] = layers.Relu()
        self.layers['Affine2'] = layers.Affine(self.params['W3'], self.params['b3'])

        self.last_layer = layers.SoftmaxWithLoss()

    def predict(self, x):
        for key in self.layers.keys():
            x = self.layers[key].forward(x)
        return x
        
    def loss(self, x, d):
        y = self.predict(x)
        return self.last_layer.forward(y, d)

    def accuracy(self, x, d, batch_size=100):
        if d.ndim != 1 : d = np.argmax(d, axis=1)
        
        acc = 0.0
        
        for i in range(int(x.shape[0] / batch_size)):
            tx = x[i*batch_size:(i+1)*batch_size]
            td = d[i*batch_size:(i+1)*batch_size]
            y = self.predict(tx)
            y = np.argmax(y, axis=1)
            acc += np.sum(y == td) 
        
        return acc / x.shape[0]

    def gradient(self, x, d):
        # forward
        self.loss(x, d)
        
        # backward
        dout = 1
        dout = self.last_layer.backward(dout)
        layers = list(self.layers.values())
        
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 設定
        grad = {}
        grad['W1'], grad['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
        grad['W2'], grad['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grad['W3'], grad['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grad

from common import optimizer

# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)

print("データ読み込み完了")

# 処理に時間のかかる場合はデータを削減 
x_train, d_train = x_train[:5000], d_train[:5000]
x_test, d_test = x_test[:1000], d_test[:1000]


network = SimpleConvNet(input_dim=(1,28,28), conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
                        hidden_size=100, output_size=10, weight_init_std=0.01)

optimizer = optimizer.Adam()

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10



for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]
    
    grad = network.gradient(x_batch, d_batch)
    optimizer.update(network.params, grad)

    loss = network.loss(x_batch, d_batch)
    train_loss_list.append(loss)

    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))               

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()

データ読み込み完了
    Generation: 10. 正答率(トレーニング) = 0.5386
                    : 10. 正答率(テスト) = 0.514
    Generation: 20. 正答率(トレーニング) = 0.5666
                    : 20. 正答率(テスト) = 0.539
    Generation: 30. 正答率(トレーニング) = 0.7254
                    : 30. 正答率(テスト) = 0.713
    Generation: 40. 正答率(トレーニング) = 0.793
                    : 40. 正答率(テスト) = 0.775
    Generation: 50. 正答率(トレーニング) = 0.8136
                    : 50. 正答率(テスト) = 0.783
    Generation: 60. 正答率(トレーニング) = 0.8538

    (中略)

    Generation: 1000. 正答率(トレーニング) = 0.9962
                    : 1000. 正答率(テスト) = 0.96

5. 最新のCNN

• AlexNetの紹介をとおして落ち穂拾い

  • Section タイトルは "最新の" CNN と書かれているが、動画講義のせつめいでは "比較的初期の" と言われている.

    • 本当に最新の持ってくると、複雑すぎるのでシンプルなものを取り扱う、ということらしい.

  • 扱う問題:

    • ImageNet と呼ばれる 画像の分類

    • 入力画像サイズ = 224x224x3, 出力クラス分類 = 1000 ?

  • 構造: 具体的な構造は実装演習のコードで示すので割愛

    • 1層目の説明で、「カーネルサイズがでかいから、一気に次の層のサイズが小さくなる」と説明されているが、kernel size による出力サイズへの影響はたかだか、kernel size -1。ストライドが4であることのほうが影響大きいのでは?

    • 畳み込み層から、全結合層への以降方法

      • AlexNet では、Flatten (複数次元データを単純に1次元ベクトルに並べ替え)

      • 後に、Global Max Pooling, Global Average Pooling などが提案された

        • 画像サイズと同じサイズの kernel をつかった Pooling

        • Flatten より Global xxx Pooling のほうがうまくいくケースが多いらしい

          • 講師の先生は、Flatten のほうが情報保持しているからうまく行きそうなのに.. 的な前置きをしていたが、その直感には賛同しかねる。情報量多いとそれだけ全結合層のパラメータ増えるので学習進みにくくなる可能性はあるし..

  • 学習方法の工夫

    • Dropout を全結合層の出力に使用

      • 畳み込み層に使う事もなくはないが、全結合層に使うケースが多いらしい

実装演習無し

取り組み概要 & 感想

取り組みの記録

今回は、実装演習にじっくり時間をかける感じでもなかったので、 Section単位で 動画みながらまとめ->実装演習 と進めていった。

• 5/7 : Day1 Section.1 までの動画、コードをざっと眺めて、レポートの要件について事務局問い合わせ。(1h)

  • レポート提出方法の"実装演習"というのが何を指しているのか不明確であったため。

  • 事務局回答を踏まえて、本ページ 冒頭に書いたようなまとめ方をすることにした。

　- Stage.1,2 動画は基本座学で、コードの内容や動画で取り上げられることはほぼなかったが、このStage.3 では動画講義中にもコードを見て動かすシーンが多発するので、エディタ上で動画を見ながらレポートをまとめつつ、コードも実行しつつのスタイルですすめる形を取ることにした.

• 5/13: プロローグ を動画みながらざっくりまとめ (0.5h)

• 5/14: Day1 Section 0, 1, 2 を動画みながらざっくりまとめ (1.5h)

• 5/15: Day1 Section 3 (1h)

• 5/16: Day1 Section 4 (1.5h)

• 5/17: Day1 Section 5 (1h)

• 5/20: Day1 のこり (1h くらい)

• 5/22: Day2 Section 1 (1.75h)

• 5/23: Day2 Section 2 (2.5h)

  • 演習でのハイパパラメータを色々試していたら時間を食った

• 5/25: Day2 Section 3 (3h)

  • 同じく、ハイパパラメータを色々試していたら時間がかかってしまった。特に Dropoutを入れると収束するまでに 必要なiterationが増えるのが大きかった。

• 5/31: Day2 Section 4,5 (2h)

• 6/1 : ステージテスト (2h)

感想ほか　

今回のステージの動画に出てきた講師の方は Stage1,2の方とは違う方。(スタートテスト前のPython講座などをやっていた方) 講師として実績はある方なのだと思うが、私とは、指導・解説の仕方のフィーリングが合わず、意図を汲み取りかねる箇所などがあった。 同じような感想を持った方は、資料の数式を正として要旨を理解し、講師の先生の言い回しや独自の説明の内容についてはあまり細かいところまで気にしすぎないのがよいかもしれない。

例えば..

• 説明で使う言葉に若干の違和感を感じることがあった

  • 一例: 重み付き和を　まぜ合わせる, シャッフルと表現。

    • "カードを交ぜる" / "醤油と塩を混ぜる" という２つの表現は、まぜたあと個々が区別できるかどうかが違う。シャッフルは前者に該当。絶対間違えだと主張するつもりはないが、なぜあえて、シャッフルという表現をつかったのかな?と1分立ち止まってしまった。

• 図の説明が独特

  • 例: 学習率の違いによって収束のしかたが異なることを手書きの図を使って説明したとき、loss 関数のグラフの傾きが異なる点でも、同じようにパラメータが変化していくような矢印を書いている。おそらく、初学者にとっては混乱を招く図の書き方だろう

• 細かい点の見間違いがちらほら

  • 例: 確認テストの細かい意味を取り違えて、おそらく想定した正解とは異なる解答を示すことがある(確認テストの5-2 など)

• 前後関係を無視した説明, 用語の使い方

  • 例: ミニバッチ勾配降下法の説明をしたあとで、確認テストでその利点を説明させる流れなのに、分散学習的な実装を想定した説明をする。箇所箇所で言っていることは正しいのだが、資料作成者が想定した流れではないと思うし、初学者はミニバッチ勾配降下法の理解に不安を持つと思う。分散学習の話するならするで、「これはまたミニバッチ勾配降下法の基礎の学習とは別の段階の話ですが、分散学習というのがあって、、」みたいな前置きをするのがいいのかな、と思う。

実装演習に関しては、やはり Stage.2 と同じで基本そのままで動いてしまうので、"勉強の仕方が上手い人" でないとさーっと通り過ぎてしまってコードから多くを学ぶことができないのではないのかな? と思った。

テストについて。他の受講生の方でちらほら 合格に苦労したという方がいたので、ケアレスミスの内容にゆっくり解いた。 全問正解だったが、必要以上に時間を書けすぎてしまったかな。。同じペースで本番やったら、問題解ききれない。

内容については 詳細は触れないが、Stage.3 にかぎらずこれまでの講義のどこかでやった内容からの出題で、特に未知の情報は無い。 出題文の日本語の意味がちょっとわかりにくいな、という出題はいくらかあったが、4択問題なので正解はまぁ導けるかな、、とは思う。 「誤ってる/正しいものを選べ」形式の設問でいくつか迷ったものがあったので、それは復習をしておこう。

計画 (前回から変更無し)

Stage.2 終了時に見直したスケジュールはほぼキープできた。 ペースは上がってきているが、ステージ3より4の方がボリュームありそうなので、 前倒しにはせず、今の所変更無しとしておく。 前評判ではステージ4のテストはめっぽう難しいらしいので、クリア前に計画見直す可能性もあるかも?

• ~2021/2/15 : スタートテスト (2021/02/07完了, 10h)

• ~2021/3/30 : ステージ1 (2021/03/30完了, 8h)

• ~2021/5/6 : ステージ2 (2021/05/06完了, 21h)

• ~2021/5/30 : ステージ3 (2021/06/02完了, 17.75h)

• ~2021/6/27 : ステージ4

• ~2021/7/4 : 復習 -> 修了テスト

• ~2021/7/15 : Eもぎライト -> 今後の計画具体化

• ~2021/7/30 : シラバスの未習箇所の学習

• ~2021/8/26 : 全体の復習

• 2021/8/27,28: E資格 受験